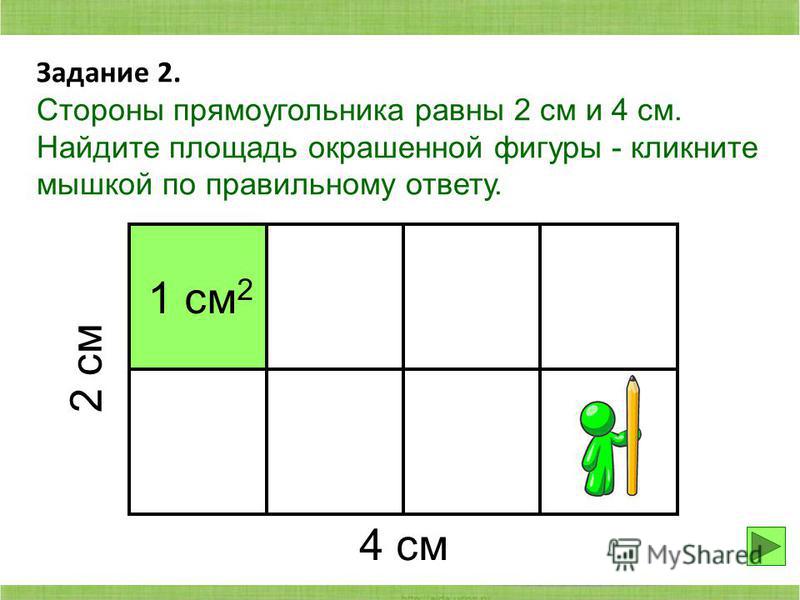
Содержание
Как вычислить площадь участка с разными сторонами
Как посчитать сотки земли и измерить площадь участка? на сайте Недвио
Сотки и гектары — это общепринятые единицы площади земельных участков. Но как понять действительные размеры участка? Если это прямоугольная территория, с ровными границами — то здесь достаточно элементарных знаний математики, а если нет — здесь без сложных расчетов и калькулятора не обойтись.
В этой статье мы рассмотрим основные методики расчета площади участков и их особенности применения.
Чему равна сотка? Сколько квадратных метров в сотке?
Сотка земли — это участок площадью 100 кв. м. (сто квадратных метров).
Почему эта единица измерения получила такое название? Есть несколько версий: кто-то считает, что «сотками» стали называть участки земли из-за их площади (100 м2 — сто метров — сотка), кто-то полагает, что термин произошел, как сотая часть гектара (1 га = 10.000 кв. м / 100). Есть и второе название этой меры измерения площади участков — «ар».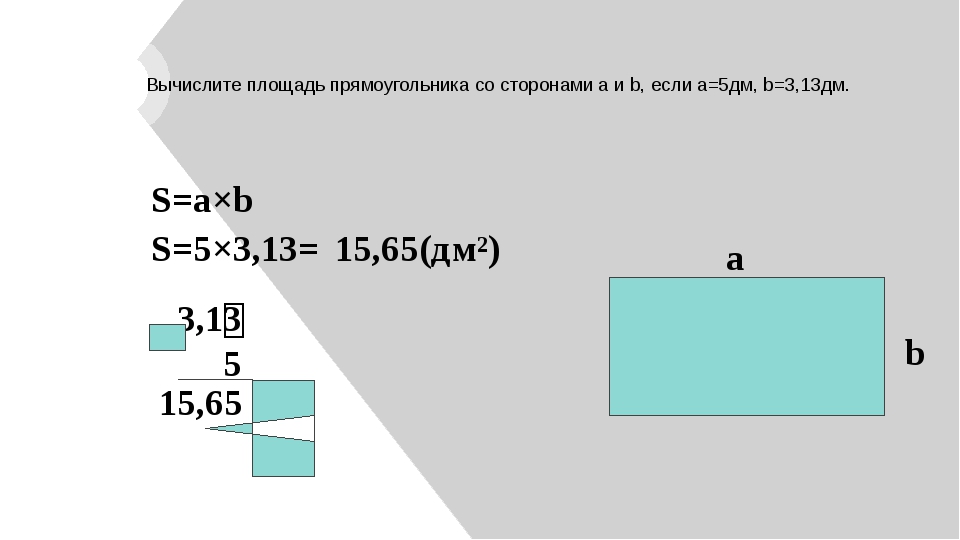 Но оно сегодня используется крайне редко.
Но оно сегодня используется крайне редко.
Мера деления участков на сотки прижилась в большинстве стран. Сотками удобно считать площадь не только земель, но и сада, огорода, дачного участка, при определении территорий для продажи и строительства.
Интересно отметить, что далеко не все страны измеряют площадь участков в сотках. В Англии и США, например, земля измеряется в акрах и квадратных ярдах, а для обозначения расстояния вместо метров используют футы и мили.
В нашей стране, термины «сотка» и «гектар» вошли в обиход только после 1917 года. До этого использовали десятины, версты и другие величины измерения.
Сегодня, в сотках меряют обычно небольшие участки. Если идет расчет размеров участков средней площади, где стороны имеют расстояния более 100 кв. метров, обычно используют единицы в 1 га (гектар). Для того, чтобы посчитать размеры больших участков принято использовать единицы площади в 1 квадратный километр (1 кв. км). Так, территории стран, областей, крупных городов обычно рассчитывают именно в км2.
Как рассчитать сколько соток на участке?
Площадь небольшой территории (как например садового участка) вполне можно рассчитать самостоятельно. Для этого чаще всего используют следующий метод:
- по углам участка ставят палки-колышки;
- затем двумя обычными рулетками измеряют расстояние в четыре стороны;
- полученные данные фиксируются и записываются на бумагу.
Что делать дальше? Возьмем пример: Допустим, мы померяли рулеткой расстояние от колышка к колышку и получили 50 метров по одной стороне, и 35 м — по второй. Согласно правилам геометрии площадь прямоугольной фигуры равна произведению сумм двух смежных сторон. Очевидно, что нам нужно умножить 50 на 35, и мы получим площадь — 1750 кв. м.
После того, как мы определили площадь в квадратных метрах, нам нужно перевести эти значения в сотки. Как мы уже говорили, сотка — это 100 кв. м земли. Поэтому, чтобы узнать площадь нашего участка в сотках нужно разделить 1750 / 100. То есть наш участок имеет размер 17,5 соток.
То есть наш участок имеет размер 17,5 соток.
Эти же правила справедливы и в обратную сторону. Так, к примеру, если вы видите объявление о продаже земельного участка размером в 9 соток — это значит, что его площадь равна 900 квадратных метров (9 * 100 = 900).
А вот с длиной сторон участков уже посложнее. 900 кв. м. — могут быть как форме квадрата (30 х 30 м), так могут быть и в форме прямоугольника (например, 20 х 45 м или 25 х 36 м), а могут и вовсе иметь разную длину сторон.
Формулы расчета площади участков. Примеры
Приведем для понимания несколько примеров расчетов:
- 10 соток нужно перевести в квадратные метры. Тогда 10 * 100 = 1000 кв. м;
- Какова площадь территории прямоугольной формы со сторонами 25 и 30 м. Считаем: 25 * 30 / 100 = 7,5 сот.;
- Каковы размеры сторон участка в 25 соток. 25 сот. — это 2500 кв. м. Вычисляем корень квадратный из 2500, получаем 50 м;
- Какова площадь участка со сторонами 20 и 10 м. Считаем: 20 × 10 = 200 кв.
 м. или 2 сотки.
м. или 2 сотки.
Наиболее сложные случаи возникают при определении размеров земельных участков неправильной формы. Для этого нужно знать размеры каждой из сторон и лучше использовать специальный калькулятор:
Как применять эти данные?
Допустим, вы планируете построить дом площадью 100 квадратных метров на участке в 8 соток. Соответственно 100 делим на 1 и получаем, то дом займет территорию в 1 сотку. Остальные 7 соток мы можем использовать по своему усмотрению: разбить огород, построить гараж, бани, теплицы и т. д.
Вы можете нарисовать план участка на бумаге, определить, где находится дом, сколько места он занимает, а также расположение других строений и насаждений.
Измерение площади участка шагами
Если при осмотре интересующей территории, у вас нет с собой измерительных приборов, и даже рулетки, можно посчитать площадь участка «на глаз». Как вариант — способ посчитать размер участка шагами.
Общеизвестно, что размер шага обычного человека — 0,7 м. Таким образом для того чтобы рассчитать сто квадратных метров, вы делаете 12-14 шагов в одну сторону, затем под прямым углом делаете такое же количество шагов в другую сторону. Квадрат в 12-14 шагов — это и есть сотка земли.
Таким образом для того чтобы рассчитать сто квадратных метров, вы делаете 12-14 шагов в одну сторону, затем под прямым углом делаете такое же количество шагов в другую сторону. Квадрат в 12-14 шагов — это и есть сотка земли.
Как измерить площадь участка палкой?
Еще один способ как можно измерить площадь — соорудить палку длиной в 1 метр (или два) и делать замеры с помощью нее.
Наиболее точной длину палки можно сделать при помощи роста тела или же какого-либо предмета, размер которого известен. Это может быть тротуарная плитка (обычно 30 см) , столбик ограждения или же можно измерить растяжкой большого и указательного пальца (приблизительно 20 см) .
Как рассчитать сотку земли при помощи палки? Очень просто. Отмерьте ей 10 раз обе стороны участка и у вас получится сто квадратных метров.
Есть и более продвинутый способ применения этого способа, когда из трех палок делается тренога или, как еще называют, «сажень». По опыту скажем, что измерять участок сажнем выходит намного быстрее.
Измерение участка рулеткой
Это самый точный и оптимальный способ. Вообще, если вы подбираете участок для покупки, возьмите за правило — всегда иметь рулетку с собой. И калькулятор.
С помощью них и вышеуказанных формул вы сможете с высокой точностью рассчитать размер практически любого участка и проверить слова продавца еще до переговоров / внесения залога.
Как рассчитать площадь участка аналитическим методом
Площадь – важнейшая характеристика участка, которая может быть необходима при различных сделках. Например, при продаже, покупке или обмене участка. Этот показатель обязательно присутствует в перечне параметров участка, зафиксированных в ЕГРН.
Виды расчета площади
Существуют следующие виды расчета площади:
Аналитический метод наиболее точен, поскольку его точность зависит только от точности полевых измерений. В двух других методах дополнительные ошибки могут появиться еще и из-за неточности планов и деформации бумаги.
В первом случае при расчете используются результаты полевых измерений координат или длин границ участка, во втором случае используются данные, полученные с плана участка, в третьем случае используется специальный прибор – планиметр.
Аналитический расчет
Наиболее полный и точный расчет можно произвести по координатам поворотных точек. Такие координаты определяются кадастровым инженером при проведении межевания участка. Вычисление таких координат производится с помощью различных методов, указанных в приказе МЭР № 518 «О требованиях в точности определения характерных точек».
Наиболее точными методами определения координат являются геодезический и спутниковый методы, для которых используются опорные межевые сети. Эти координаты можно получить в выписке из ЕГРН.
При этом площадь участка вычисляется по формуле Гаусса:
S=0,5*(x1-1+ x2y3+…+ xn-1yn+ xny1- x2y1- x3y2-…- xnyn-1- x1yn),
где xi, yi –координаты i-той опорной точки.
Для проведения такого сложного расчета надо знать координаты опорных точек земельного участка.
На практике часто требуется оценить площадь земельного участка на месте. При этом в качестве средства измерения может быть только рулетка.
В этом случае порядок расчета площади зависит от геометрической формы участка. Для простой формы участка площадь считается в соответствии с простейшими правилами геометрии.
Треугольная форма
Например, площадь участка в виде прямоугольного треугольника рассчитывается по формуле:
S=0,5*a*b,
где а и b – длина двух сторон участка.
Для треугольника, не являющимся прямоугольным, площадь равна:
S=0,5*h*b,
где b – основание фигуры, а h – его высота.
На практике не всегда удается измерить высоту треугольника, отображающего форму участка. Проще измерить длины сторон. В этом случае для расчета площади участка используется формула Герона:
где а,b и c – стороны треугольника, а p=0,5*(a+b+c) – полупериметр треугольника.
Четырехугольная форма
Для участка в виде прямоугольника площадь равна:
S=a*b,
где а и b – размеры длинной и короткой сторон прямоугольника.
Для участка в форме трапеции площадь равна:
S= (a+b)/2*h,
где а и b – длины оснований фигуры, а h – ее высота.
В общем случае площадь участка в виде четырехугольника можно определить по формуле:
S=0,5*d1*d2*sin α,
где d1и d2 – диагонали фигуры, а α – угол между ними.
В некоторых случаях площадь четырехугольного участка можно вычислить по его четырем сторонам. В частности, если четырехугольник, отображающий форму участка, может быть вписан в окружность (то есть суммы его противоположных углов равны между собой и равны 180°), то его площадь вычисляется по формуле Брахмагупты, подобной формуле Герона для треугольника:
где а,b,c и d – стороны четырехугольника, а p=0,5*(a+b+c+d) – его полупериметр.
Многоугольная форма
Для участка со сложным контуром основной прием расчета его площади состоит в разбиении сложной фигуры на простые (например, треугольники и прямоугольники). Вычисленные площади простых фигур затем суммируются.
Вычисленные площади простых фигур затем суммируются.
Возможный алгоритм действий для определения площади участка, имеющего форму многоугольника, состоит в следующем:
- Выбрать точку внутри многоугольника и забить в нее колышек.
- От колышка к каждой вершине многоугольника протянуть бечевку.
- С помощью рулетки измерить длины каждой из сторон всех образовавшихся треугольников.
- По формуле Герона вычислить площади треугольников.
- Просуммировав площади треугольников, получить величину площади участка.
Если многоугольник не имеет внутренних углов, больших 180 градусов, центральную точку можно совместить с одной из вершин. В этом случае количество образовавшихся треугольников уменьшится на 2, что упростит задачу.
В некоторых случаях, когда участок имеет слишком сложную форму и много опорных точек, более правильным приемом является использование замеров по азимуту. При этом для каждой опорной точки по контуру границы участка определяется размер угла по азимуту и расстояние до следующей опорной точки. Измерения производятся по часовой стрелке. После окончания измерений все результаты загружаются в специальную программу, которая с большой точностью рассчитывает площадь участка.
Измерения производятся по часовой стрелке. После окончания измерений все результаты загружаются в специальную программу, которая с большой точностью рассчитывает площадь участка.
Как рассчитать сотки земли на участке? Чему равна сотка?
Слово «сотка» широко бытует в неофициальном общении людей, особенно тех, что связаны с земельными участками. Да-да, какой же дачник-огородник не знает, сколько соток земли на его участке? Уж старое поколение точно и наизусть помнит о своих трех или шести сотках!
И хотя в в официальных земельных документах требуется отмечать площадь участков только в гектарах, тем более при купле-продаже, всё же для людей привычнее слышать и считать землю под огород именно в сотках.
Для взаимодействия с кадастровыми инстанциями приходится напрягаться и пересчитывать площадь участка именно в гектарах (га). В этом материале мы предлагаем разобраться в терминологии и единицах измерения земли, выяснить, что такое собственно «сотка» и каково её соотношение с гектаром.
Сколько квадратных метров в одной сотке?
Какие бы ни были причины уточнения площади вашего земельного участка, размеры которого вам известны в сотках, классический перевод из соток в метры будет проходить по схеме:
площадь размером в 1 «сотку» = 100 квадратным метрам (1 сотка = 100 м2).
Как замерить площадь участка земли простой формы?
Измерение правильно начинать с замера сторон участка. Забив по углам участка колышки, при помощи рулетки, делаете точные их замеры в длину и ширину. Если участок правильной геометрической формы, то понадобятся только две его стороны — длина и ширина. Результаты измерений лучше записать в блокнот или занести в компьютер.
Но если ваш участок оказался асимметричным — нужно в таком случае замеры всех четырех его сторон и углов в градусах, либо длины диагоналей — тоже под запись.
Если ваш огород неправильной формы (НЕ квадратный или НЕ прямоугольный участок), то методика измерения земельного участка немного сложнее, чем умножение длины и ширины, но вполне под силу обычному человеку без специального образования.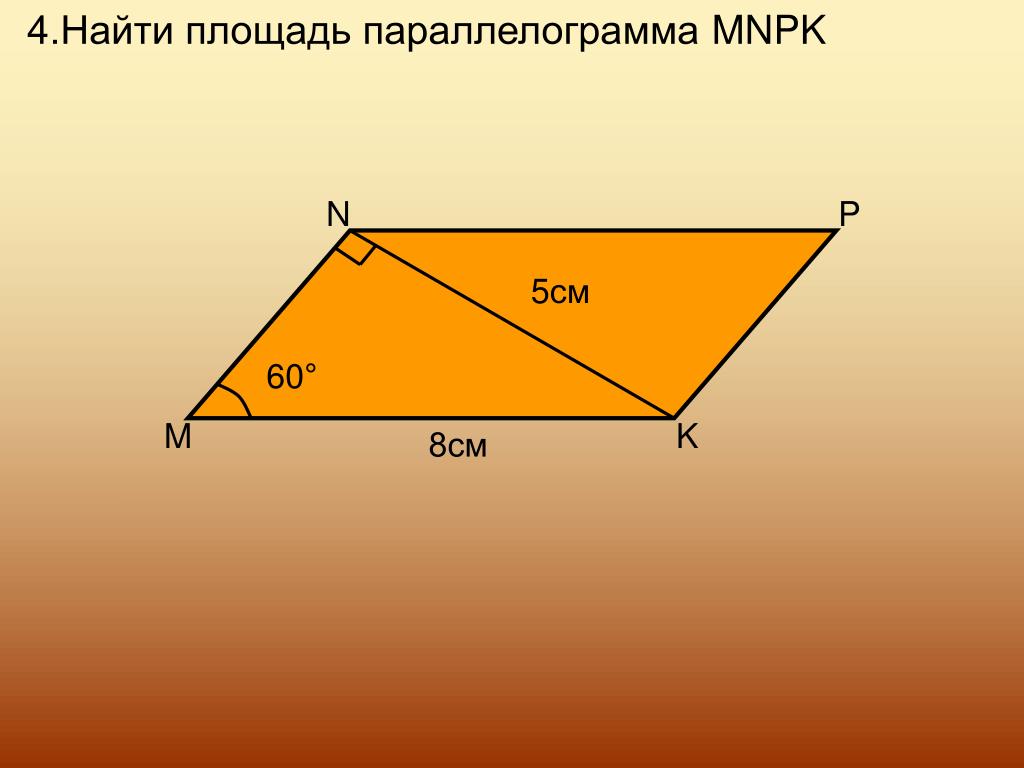
Как определить размер участка в квадратных метрах
Чтобы расчет оказался как можно более точным, понадобятся рулетка, несколько колышков и блокнот для записи результатов измерения. Весь ход требуемого расчета идет по законам курса школьной геометрии, который гласит, что для точного определения площади прямоугольной фигуры следует умножить его ширину на длину, например:
Например, если длина вашего участка земли 70 метров, а ширина 40 метров, то площадь можно рассчитать как S = 70м * 40м = 2800 м2, то есть в данном случае площадь вашей земли 2 800 квадратных метров.
Как перевести метры в сотки
Учитывая, что 1 сотка равна 100 м2, идем обратным путем для перевода данных из метров в сотки. Это позволит получить корректные результаты замера площади данной земельной делянки. При расчете количества квадратных метров в сотке нужно получившийся результат разделить на 100, например:
- площадь участка — 1000 м2;
- 1000 м2 разделить на 100;
- количество соток — 10
Если ваш участок неправильной геометрической формы, но вами правильно посчитана его площадь в квадратных метрах, методика вычисления размера в сотках остается прежней. Участки с большой площадью обычно измеряются гектарами, каждый из которых состоит из 10 000 квадратных метров или 100 соток.
Участки с большой площадью обычно измеряются гектарами, каждый из которых состоит из 10 000 квадратных метров или 100 соток.
Расчет площади земельного участка онлайн калькулятором
На сегодня в сети довольно много сервисов и онлайн-калькуляторов, позволяющих рассчитать площадь земельного участка, достаточно воспользоваться одной из поисковых систем, например Яндекс.
Имейте в виду, что онлайн калькулятору расчета площади участка земли понадобится точные размеры всех сторон участка в метрах, чтобы его алгоритм справился с точным расчетом площади вашего участка земли.
Как рассчитать площадь участка сложной формы?
Сложнее поддается расчету участок неправильной формы и только лишь размеров сторон будет недостаточно для вычисления площади участка сложной формы. Здесь вам потребуется знать размеры и всех сторон огорода, и размер диагоналей Чуть проще, если один из углов участка составляет 90 градусов.
Вот пример расчета соток земли дачного участка сложной формы:
Размеры сторон земельного участка, в метрах
- Сторона A-B = 69 метров,
- Сторона B-C = 46 метров,
- Сторона C-D = 87 метров,
- Сторона D-A = 35 метров,
- Левый нижний угол прямой (90 градусов)
По этим данным можно определить длины диагоналей B-D и A-C, и рассчитать площадь участка = 3035 квадратных метров (или 30,35 соток).
5 КОММЕНТАРИИ
Вот это информация, достойная доверия и уважения, которая многим поможет выполнить правильный замер площади своего земельного участка или проверить результаты такого замера, чтобы в них не сомневаться.
У меня участок ровно прямоугольный, поэтому брал веревку, замерял стороны веревкой, потом небольшой рулеткой уже мерял длину веревки и умножал длину на ширину, как в школе на уроках геометрии.
Знаете ли вы, что измерить сотку шагами довольно легко, зная размер вашего шага в сантиметрах (метрах). Так, например, в среднем, обычный шаг взрослого человека равен 60 сантиметрам (0,6м), таким образом вы можете высчитать количество шагов, необходимых чтобы пройти вдоль ширины и длины участка земли, затем умножить на длину вашего шага (полезно её измерить заранее и помнить/знать) на число шагов, в результате узнаете длину и ширину участка в метрах. Перемножив длину и ширину земельного участка вы определите его площадь с помощью шагов и пары математических вычислений. Например, длина вашего огорода 200 шагов, а ширина 100 шагов, зная, что шаг это 0,6 метра, легко узнать, что ширина вашего дачного участка 60 метров (100 шагов х 0,6 метра), а длина 120 метров (200 шагов х 0,6 метра), таким образом площадь вашего огорода равна 60 х 120 метров = 7 200 квадратных метров, а чтобы вычислить площадь в сотках достаточно полученный результат разделить на 100, в итоге в сотках ваш земельный участок составляет 72 сотки. И посчитали вы этот результат с помощью шагов и пары операций умножения и деления.
Например, длина вашего огорода 200 шагов, а ширина 100 шагов, зная, что шаг это 0,6 метра, легко узнать, что ширина вашего дачного участка 60 метров (100 шагов х 0,6 метра), а длина 120 метров (200 шагов х 0,6 метра), таким образом площадь вашего огорода равна 60 х 120 метров = 7 200 квадратных метров, а чтобы вычислить площадь в сотках достаточно полученный результат разделить на 100, в итоге в сотках ваш земельный участок составляет 72 сотки. И посчитали вы этот результат с помощью шагов и пары операций умножения и деления.
Добрый день, такой вопрос: огород 15*30, по расчётам 4,5 сотки, если изменю размеры к примеру 10*35 то получится 3,5 сотки, а если сделать 20*25 то 5 соток?
Да, всё верно, площадь прямоугольного участка это произведение его длины на его ширину. Таким образом если длина будет 35 метров, а ширина 10 метров, то площадь составит 350 м2, то есть три с половиной сотки.
Онлайн калькулятор: Площадь многоугольника
Пример многоугольника
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площадь многоугольника
addimport_exportmode_editdelete
Стороны и диагонали
Размер страницы: chevron_leftchevron_right
Стороны и диагонали
Сохранить
Отменить
Импортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5
Загрузить данные из csv файла
Импортировать
Назад
Отменить
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить
close
content_copy Ссылка save Сохранить extension Виджет
Онлайн калькулятор площади земельного участка
Точность расчетов площади
При определении площади участка необходимо учитывать погрешности расчета площади.
В частности, если площадь участка рассчитана по координатам поворотных точек, то разница между расчетным и зафиксированным в ЕГРН значениями площади ЗУ не должна быть больше допустимой величины (dSдоп).
В нормативных документах эта величина определена следующим образом:
dSдоп=3,5*Mt*√Sу где:
- Mt – погрешность (СКП) расположения поворотной точки;
- Sy-площадь участка.
При этом если dS превышает допустимую величину, то необходимо провести проверку точности координат и методики расчета площади участка.
Если же dS оказывается меньше допустимого значения, то за окончательное значение площади может быть принято расчетное значение площади с указанием допустимого значения dPдоп.
Пример.
Вычисленная площадь участка № 103 снт “Изобретатель” составила 594 кв. м. По документам площадь участка равна 600 кв. м.
СКП Мt при межевании для садоводческих товариществ определена нормативно (приказ МЭР №518) и равна 20 см. Тогда:
dS = 600-594= 6 кв. м
dSдоп=3,5*0,2* √600=17,14 кв. м
Окончательное значение площади участка №103 Sy=594±17 кв. м.
Не нашли ответа на свой вопрос? Звоните на телефон горячей линии 8 (800) 350-34-85.
Это бесплатно.
Юрист. Практика в сфере недвижимости, тудового права, семейного права, защите прав потребителей
Как применять эти данные?
Допустим, вы планируете построить дом площадью 100 квадратных метров на участке в 8 соток. Соответственно 100 делим на 1 и получаем, то дом займет территорию в 1 сотку. Остальные 7 соток мы можем использовать по своему усмотрению: разбить огород, построить гараж, бани, теплицы и т. д.
Вы можете нарисовать план участка на бумаге, определить, где находится дом, сколько места он занимает, а также расположение других строений и насаждений.
Измерение площади участка шагами
Если при осмотре интересующей территории, у вас нет с собой измерительных приборов, и даже рулетки, можно посчитать площадь участка «на глаз». Как вариант — способ посчитать размер участка шагами.
Общеизвестно, что размер шага обычного человека — 0,7 м. Таким образом для того чтобы рассчитать сто квадратных метров, вы делаете 12-14 шагов в одну сторону, затем под прямым углом делаете такое же количество шагов в другую сторону. Квадрат в 12-14 шагов — это и есть сотка земли.
Квадрат в 12-14 шагов — это и есть сотка земли.
Как измерить площадь участка палкой?
Еще один способ как можно измерить площадь — соорудить палку длиной в 1 метр (или два) и делать замеры с помощью нее.
Наиболее точной длину палки можно сделать при помощи роста тела или же какого-либо предмета, размер которого известен. Это может быть тротуарная плитка (обычно 30 см) , столбик ограждения или же можно измерить растяжкой большого и указательного пальца (приблизительно 20 см) .
Как рассчитать сотку земли при помощи палки? Очень просто. Отмерьте ей 10 раз обе стороны участка и у вас получится сто квадратных метров.
Есть и более продвинутый способ применения этого способа, когда из трех палок делается тренога или, как еще называют, «сажень». По опыту скажем, что измерять участок сажнем выходит намного быстрее.
Измерение участка рулеткой
Это самый точный и оптимальный способ. Вообще, если вы подбираете участок для покупки, возьмите за правило — всегда иметь рулетку с собой.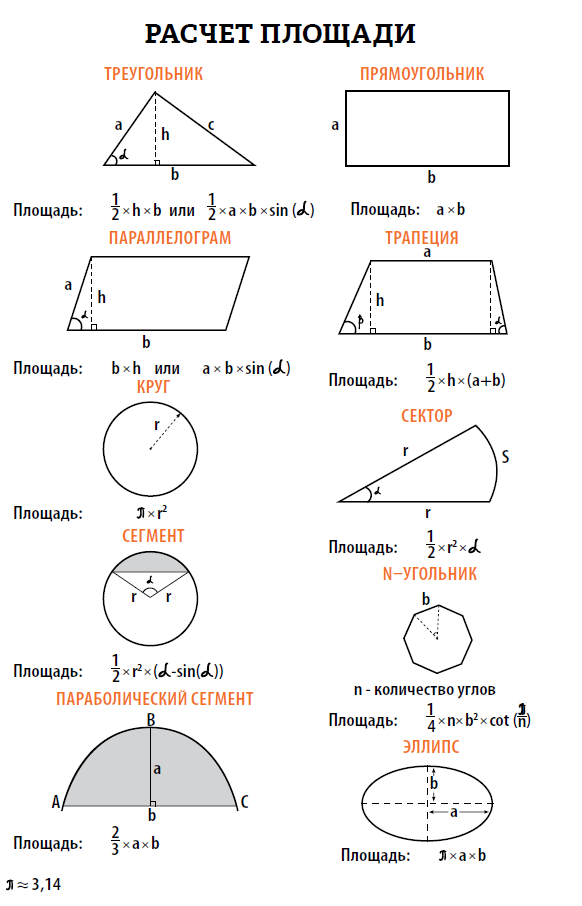 И калькулятор.
И калькулятор.
С помощью них и вышеуказанных формул вы сможете с высокой точностью рассчитать размер практически любого участка и проверить слова продавца еще до переговоров / внесения залога.
Купить лазерную рулетку
Была ли эта статья для вас полезной? Пожалуйста, поделитесь ею в соцсетях:
Не забудьте добавить сайт Недвио в Закладки. Рассказываем о строительстве, ремонте, загородной недвижимости интересно, с пользой и понятным языком.
Расчет площади многоугольника онлайн
Калькулятор считает площадь многоугольника по введенным вами сторонами и диагоналям, главное чтобы диагонали делили многоугольник на несколько треугольников, которые в свою очередь не пересекались бы между собой.
И так, глядя на рисунок, можно сразу представить, что площадь данного многоугольника будет равна сумме площади трех треугольников, расположенных внутри многоугольника.
Для начала расчетов вам придется внимательно внести в таблицу значения сторон ваших треугольников.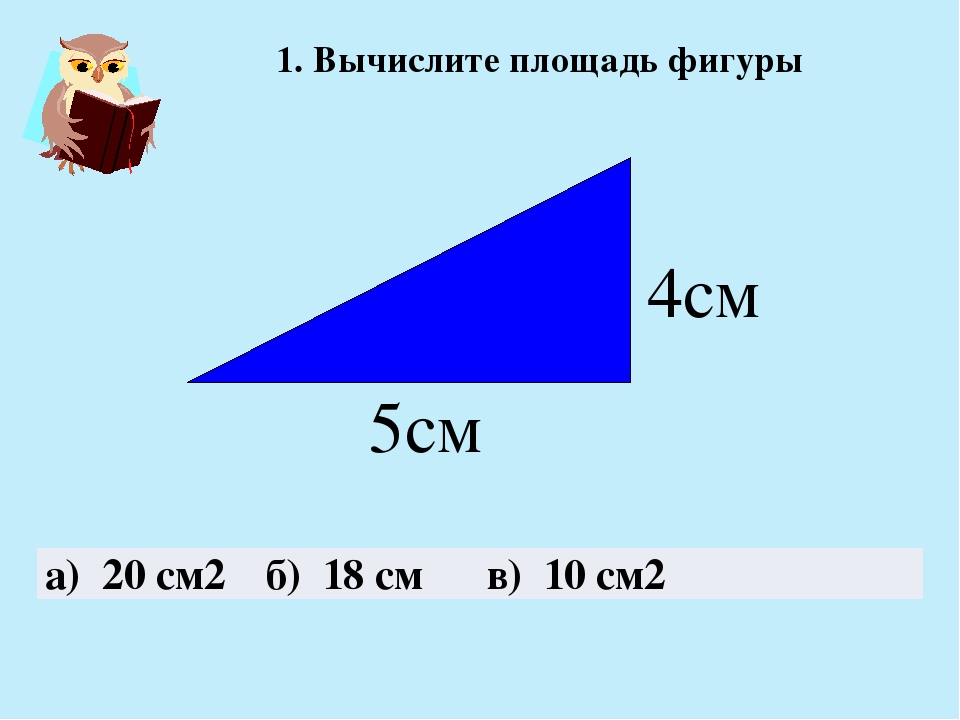
Все остальное калькулятор сделает за вас. Пользуйтесь.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B. C.
C.
%1 century
An error occurred while importing data on line% 1.
Value: ‘%2’.
Error:
%3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Как рассчитать площадь комнаты самостоятельно без ошибок
Если вы решили сделать ремонт в квартире или доме, в первую очередь необходимо выбрать материалы для отделки и понять, сколько же их нужно. Для этого нужно правильно рассчитать площадь всех поверхностей в квартире. Конечно, можно прибегнуть к помощи профессионалов, потратив при этом лишние деньги. А можно заняться этим самостоятельно. Тому, как рассчитать площадь комнаты разной формы, посвящена данная статья.
План комнаты, размер которой необходимо считать в два этапа путем сложения величин
Читайте в статье
Для чего необходимо знать площадь комнаты и что потребуется для расчетов?
В каких же случаях необходимо рассчитывать площадь комнаты?
- Конечно, в первую очередь для определения количества расходных материалов для ремонта. Многие закупают их с запасом, а излишки возвращают в магазин. Однако в данном случае теряется много времени, к тому же не все магазины предоставляют такую услугу. Поэтому целесообразней правильно высчитать площадь всех поверхностей перед покупками.
Чтобы у вас не осталось много обрезков, правильно рассчитайте площадь стен, которые требуют оклейки
- Кроме того, зная площадь, проще распланировать свой бюджет. Ведь даже стоимость работ наемных работников в большинстве случаев зависит от того, сколько квадратных метров они должны обработать.
- Количество осветительных приборов также зависит от площади. Однако в большинстве случаев к сложным расчетам при выборе светильников не прибегают, данный вопрос обычно решается опытным путем.

Пример недостаточного освещения в ванной комнате
- И последнее. Одна из главных величин в квартире – объем помещений (при этом необходимо площадь умножить на высоту), ведь в зависимости от него подбирают климатическое оборудование.
Мощность кондиционера в первую очередь зависит от объема помещения
Важно! Обязательно проверьте площадь при покупке квартиры, особенно, если вы купили ее в новостройке. Ведь от нее зависит размер коммунальных платежей и зачастую стоимость самой жилплощади. Например, застройщик (в случае долевого участия в строительстве) обязан возместить стоимость недостающих квадратных метров.
Таким образом, существует огромное количество причин, по которым необходимо правильно высчитать площадь помещения. Но с чего же начать? Сначала нужно подготовить измеряемое помещение и инструменты.
Измерения желательно проводить в полностью освобожденном помещении. Если такой возможности нет, расчистите хотя бы участки около стен, ведь именно вдоль них будут проводиться замеры.
Обязательно отодвиньте всю крупную мебель от стен, которые вы будете измерять
Важно! Если комната прямоугольная, перед началом замеров проверьте правильность ее формы. Для этого сравните противоположные диагонали. Если они равны, перед вами правильный равносторонний прямоугольник.
Итак, для определения площади помещения необходимы следующие приспособления:
- Рулетка. Конечно, электронное приспособление удобней, но оно имеет большую погрешность. Кроме того, такой рулеткой не измерить сложные формы, при работе с выступающими элементами также могут возникнуть проблемы. Поэтому оптимальный набор – простая рулетка и линейка. Главное – проверить их точность, так как многие старые или детские приспособления имеют приличную погрешность.
- Карандаш.
- Листок бумаги для вычислений и записи результатов.
- Калькулятор.
Кроме того, вам может понадобиться длинная линейка для проверки ровности стен.
Как высчитать квадратный метр?
В квадратных метрах в большинстве случаев вычисляется площадь любой поверхности. Так как рассчитать квадратный метр?
Так как рассчитать квадратный метр?
Для начала, если комната прямоугольная, необходимо измерить ее длину и ширину. При этом желательно использовать рулетку с нанесенными делениями сантиметров и миллиметров. Если вам удалось найти только линейку с футами, не беда, их легко можно перевести в квадратные метры.
Далее две полученные величины в сантиметрах переводятся в метры (сразу это сделать проще) путем деления на 100. Далее две величины перемножаются, полученная величина и есть площадь комнаты в квадратных метрах. Если у вас футы, сначала перемножьте полученные значения, таким образом вы получите квадратные футы. Затем для перевода в м2 умножьте полученную величину на 0,093 (если измерения были сделаны в ярдах, умножьте результат на 0,84). В данном случае для расчета квадратных метров калькулятор – отличное решение.
Таблица перевода квадратных метров в другие популярные меры площади
Интересно! В интернете существует множество онлайн калькуляторов квадратных метров для вычисления площади помещения.
Если компьютер под рукой, такой способ будет самым быстрым.
Когда цифра получена, округлите ее до 2 знаков после запятой, более точное значение будет излишним.
Как посчитать площадь комнаты самостоятельно?
Как рассчитать площади всех помещений в квартире?
Идеальная комната прямоугольной формы – большая редкость. Как узнать площадь помещения с выступами, нишами или криволинейными скосами? Самое простое – измерить длины всех стен, а так же углы между ними, после чего начертить план вашей комнаты на листке бумаги (масштаб при этом, скорее всего, подойдет 1:100, то есть одному сантиметру на бумаге будет соответствовать один метр в помещении). Затем необходимо разделить помещение на правильные фигуры (прямоугольника, треугольники, круги и так далее), если это возможно, и пользуясь формулами расчета площади, определить квадратуру каждого участка.
Основные формулы для вычисления площади популярных геометрических фигур
Ниже приведены самые популярные фигуры, описания методик расчета которых, помогут ответить на вопрос: «Как вычислить площадь комнаты самостоятельно?».
Как найти площадь прямоугольника?
Как вычислить площадь прямоугольника самостоятельно? Комната правильной прямоугольной формы – наиболее простой случай. Для расчета площади прямоугольника достаточно перемножить его длину и ширину. Однако свои нюансы в такой ситуации тоже есть:
- После измерения одной из сторон мерят вторую необходимо строго перпендикулярно. В противном случае измерения могут получиться с существенной погрешностью.
- Чтобы избежать неточностей, меряйте обе параллельные стены, так как часто их длины несколько разные, а для точности желательно взять их среднее арифметическое. То есть сложить их значения и разделить на 2.
- Не забудьте вычесть из полученной площади всевозможные выступы (или прибавить ниши).
Интересно! В интернете существует множество программ для вычисления площади прямоугольника, онлайн калькулятор – самая простая и удобная из них.
Пример расчета площади простой прямоугольной комнаты
Калькулятор расчета площади четырехугольного помещения
Как посчитать площадь треугольников (прямоугольных и других)?
В некоторых случаях углы комнаты сильно скошены. Тогда при обрисовке плана и разделении его на фигуры появляются элементы треугольной формы. Как вычислить площадь треугольников?
Тогда при обрисовке плана и разделении его на фигуры появляются элементы треугольной формы. Как вычислить площадь треугольников?
Старайтесь, чтобы все треугольники на вашей схеме быль прямоугольными. В противном случае, посчитать площадь треугольника будет сложнее, а результат будет с большей погрешностью.
Основные формулы расчета площади треугольников
По сути, прямоугольный треугольник – это половина прямоугольника, поэтому, чтобы найти площадь прямоугольного треугольника, необходимо перемножить длины его катетов (сторон, прилегающих к прямому углу) и разделить полученную величину на 2. Если фигура оказалась всё-таки не прямоугольной, можно воспользоваться (в зависимости от того, какие величины известны) одной из следующих формул:
- S=a*h/2, где h – высота треугольника, а – сторона, к которой она опущена.
- S=a*a*sina/2. Данная формула подходит для равнобедренного треугольника (то есть с двумя одинаковыми сторонами), где а – длина одной из одинаковых сторон, а угол а – угол между одинаковыми сторонами.

- S=a*b*sina/2. Также формула для равнобедренного треугольника, а – одна из одинаковых сторон, b – третья сторона, угол а – угол между a и b.
Кроме того, любой треугольник можно попробовать разделить на несколько прямоугольных фигур. Для этого проведите линию из вершины к противоположной стороне фигуры, чтобы она образовала с ней прямой угол.
Калькулятор расчета площади треугольного помещения
Расчет площади трапеции
Трапеция – это фигура, имеющая четыре стороны, две из которых являются параллельными, а две – нет. Как рассчитать площадь трапеции самостоятельно? Можно пойти двумя путями:
- Разделить трапецию на треугольники и прямоугольник (в некоторых случаях получится всего один треугольник + прямоугольник), высчитать площадь каждой фигуры, сложить их, тем самым рассчитав площадь трапеции.
- Воспользоваться несложной формулой: S= (a+b)*h/2, где а и b – параллельные стороны фигуры, h – высота (кратчайшее расстояние) между ними.

Схема трапеции
Формула для расчета является универсальной, то есть от направления и размера боковых граней ничего не меняется. Главное – правильно измерить высоту фигуры, для этого сделайте замеры в нескольких местах.
Как вычислить площадь круга?
В комнатах (особенно в гостиных) довольно часто бывают круглые выступы, поэтому важно уметь правильно рассчитать площадь круга. При этом главное – узнать радиус окружности. Для этого измерьте расстояние от края дуги до центра виртуального круга, проведя линию между самыми дальними точками фигуры.
Теперь для расчета площади круга воспользуемся формулой: S=πR2, где π – постоянная величина 3,14, R – радиус окружности.
Схема круга
Расчет площади сегмента круга
Определение площади сегмента круга – задача сложнее. Для начала определимся, что же такое сегмент? Это часть круга, ограниченная хордой (линией, началом и концом которой случат точки от радиуса на окружности).
В первую очередь необходимо найти центр круга, чаще всего сделать это проще экспериментальным путем. Например, попросив друга стать на место предполагаемого центра, дать ему в руки один конец рулетки. Самому же описывать предполагаемую окружность. Таким образом, расчертив необходимый сегмент, можно приступать к расчету площади сектора круга. Формула довольно сложная:
Формула расчета площади сегмента круга
Поэтому целесообразней будет воспользоваться онлайн-расчетом в интернете.
Как посчитать площадь комнаты: порядок действий
Итак, что же нужно сделать, чтобы рассчитать площадь пола в комнате? Порядок действий:
- Подготовительный этап. Необходимо приготовить все инструменты и приспособления, а так же расчистить комнату.
- Измерения. Измерьте длину всех стен в комнате. При этом обратите особое внимание на углы, если они не прямые, непременно запишите их значение.
- Запись результатов. Можно пойти двумя путями: начертить план на листке или нанести размеры непосредственно на пол (если комната находится в стадии черновой отделки).

- Вычисления. При этом если вычисления осуществляются путем расчета отдельных фигур, сложите их очень внимательно, ничего не забыв и следя за тем, чтобы фигуры не находили друг на друга. Основные формулы и порядок расчетов описаны выше, поэтому с данным пунктом проблем возникнуть не должно.
Важно! Измерьте каждую длину как минимум два раза, так вы сможете избежать неточностей и ошибок.
Пример:
Пример комнаты неправильной формы
На рисунке ниже представлена неровная комната. Как посчитать квадратные метры в данном случае? Необходимо выполнить следующий порядок действий:
- Находим площадь прямоугольника, не учитывая его скос в верхнем правом углу. Для этого длину 2,5 умножаем на ширину 1,75, получается 4,375 м2.
- Находим площадь скошенного участка, это прямоугольный треугольник, поэтому получается: 0,57*0,57/2=0,162.
- Вычитаем из первой величины вторую: 4,375-0,162=4,213 м2.

- Округляем до сантиметров: 4,21 м2.
Как посчитать площадь стен?
Ни один ремонт не проходит без замены обоев или покраски стен, ведь эта самая заметная поверхность любой комнаты. Для придания стенам привлекательного вида часто требуется провести несколько этапов ремонтных работ: выравнивание при помощи штукатурки и шпаклевки, грунтовка, финишная отделка (покраска, поклейка обоев, нанесение декоративной штукатурки). На все это требуется большое количество материалов, поэтому важно заранее знать, сколько их нужно и каких денег это будет стоять.
Для этого необходимо правильно рассчитать площади стен комнаты (калькулятор, рулетка, линейка и лист бумаги – все это понадобится вам для работы в обязательном порядке).
Порядок действий:
- Определяем периметр. Как рассчитать периметр комнаты самостоятельно и правильно? Главное – делать измерения не только по плинтусам у пола, но и в середине и в верхней части стены, так как в большинстве как современных, так и старых домов стены не отличаются идеальной ровностью.
 При этом может возникнуть проблема с определением длины криволинейного участка (например, части окружности). Конечно, можно воспользоваться специальными формулами для расчетов, но проще приложить плотно к стене гибкую рулетку и аккуратно зафиксировать ее показание. Все полученные величины необходимо сложить.
При этом может возникнуть проблема с определением длины криволинейного участка (например, части окружности). Конечно, можно воспользоваться специальными формулами для расчетов, но проще приложить плотно к стене гибкую рулетку и аккуратно зафиксировать ее показание. Все полученные величины необходимо сложить.
Важно! При расчете периметра обязательно пользуйтесь уровнем (особенно, когда проводите измерения в середине стены).
Измерения должны проводиться не только на одной высоте
- Теперь необходимо измерить высоту помещения. Для этого опять же воспользуйтесь уровнем и начертите строго вертикальную линию на стене. Если уровня под рукой не оказалось, не беда, можно сделать вертикальный отвес: к нитке привязать что-либо тяжелое (например, болтик) а держать ее у потолка. Под действием силы тяжести нитка натянется вертикально вниз, а вы (или ваш помощник) сможете начертить вертикаль.
- Перемножьте полученные величины, это и будет площадью стен вашей комнаты.

Отвес можно не только сделать своими руками, но и купить в специализированном магазине
Важно! Если вы не уверены в ровности потолков, или в данном помещении он является многоуровневым, необходимо считать каждую стену по отдельности.
Пример многоуровневого потолка
- Теперь необходимо вычесть из полученного значения площадь оконных и дверных проемов (делайте это по откосам). В некоторых случаях окна имеют круглую или треугольную формулу, тогда необходимо воспользоваться формулами, приведенными выше.
Пример дизайнерских круглых окон в комнате
Общие рекомендации
Кроме всего вышесказанного стоит отметить еще несколько важных моментов, на которые стоит обратить внимание при измерении комнаты:
- Во время измерения дверных и оконных проемов не стоит надеяться на правильность их формы. Лучше несколько раз все перепроверить для исключения ошибок и погрешностей.
- При расчете расхода строительных материалов не забудьте о том, что некоторых из них понадобится несколько слоев, то есть полученный размер комнаты умножаем на несколько единиц перед покупками.

- При покупке обоев обратите внимание, нужно ли будет подгонять рисунок, если да, берите их с большим запасом. Специалисты рекомендуют даже однотонные обои брать с запасом, так как цвет разных партий несколько расходится, и докупить подходящий материал, возможно, будет сложно.
- При расчете высоты помещения необходимо знать, окончательная ли это высота пола, или он будет подниматься за счет выравнивания или покрытия. Данный момент очень важен, так как в некоторых случаях пол может подняться даже на 10-15 сантиметров из-за выравнивания слишком кривого пола, утепления, шумоизоляции и так далее.
Пример многослойного покрытия пола
Заключение
Измерение площади комнаты – процесс трудоемкий, но не сложный. Поэтому нет смысла вызывать специальную бригаду, при наличии минимального набора инструментов с этой задачей вполне можно справиться самостоятельно.
ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями
Площадь в Автокаде/AutoCAD.
 Как в Автокаде посчитать площадь
Как в Автокаде посчитать площадь
Рассмотрим, как в Автокаде измерить площадь. В первую очередь, советую ознакомиться с видеоматериалом, в котором я рассматриваю рациональный способ определения/измерения площади для объектов любой формы. Суть данного подхода состоит в том, чтобы определить площадь штриховки в Автокаде, которая и будет соответствовать искомому параметру для нужного контура (см. урок про площадь в Автокаде 2014).
Как найти площадь в Автокаде стандартным способом?
Определить площадь в Автокаде можно с помощью стандартного инструмента, который расположен на вкладке «Главная» — панель «Утилиты» — ниспадающий список «Измерить» — команда «Площадь» (см. рис.).
После выбора команды следует указать точки по периметру фигуры. Значение площади отобразится в Журнале командной строки. Там же появится и периметр объекта. Площадь отображается в мм2. Позже рассмотрим, как ее переводить в м2.
Особый интерес представляют субопции команды «Площадь»:
- оБъекты — для отображения площади нужно указать контур замкнутой фигуры;
- Добавить площадь — позволяет подсчитывать площадь сразу нескольких объектов.
 Для этого нужно активировать данную субопцию, после чего здесь же обратиться к параметру «объекты» и в графическом поле выбрать замкнутые фигуры в нужном количестве.
Для этого нужно активировать данную субопцию, после чего здесь же обратиться к параметру «объекты» и в графическом поле выбрать замкнутые фигуры в нужном количестве.
ПРИМЕЧАНИЕ: Читайте, как в AutoCAD объединить объекты в цельные 2D примитивы.
- Вычесть площадь — действие противоположное. Позволяет убрать объекты из ранее выбранных для подсчета общей площади.
Как изменить единицы измерения площади в AutoCAD/Автокад?
Как в Автокаде померить площадь — мы уже знаем, однако значения отображаются в мм2, а это не очень удобно. Чтобы перевести их в привычные м2, воспользуемся быстрым калькулятором. В свободном месте графического пространства нажимаем ПКМ и выбираем «БыстрКальк» (см. рис.).
Журнал командной строки можно увеличить путем растягивания его границ с помощью мышки. Далее находим нужное значение площади/периметра, копируем его (Ctrl+C) и вставляем значение в калькулятор. Здесь следует немного поработать со списком «Преобразование единиц» (см. рис.).
Здесь следует немного поработать со списком «Преобразование единиц» (см. рис.).
Нажав на знак «+» возле «Преобразование единиц», нужно установить «Тип единиц», выбрав из списка «Площадь». Далее следует изменить значение поля «Преобразовать из» на «Квадратные миллиметры». Чтобы преобразуемое значение отобразилось в соответствующем поле, достаточно щелкнуть ЛКМ внутри этого поля (см. рис.).
При таком подходе преобразование единиц площади из мм2 в м2 выполняется автоматически.
Как узнать площадь в Автокаде через свойства объекта?
Подсчет площади в Автокаде выполняется автоматически и для стандартных замкнутых примитивов, таких как окружности, прямоугольники или, что намного интереснее, полилинии, создающей контур, данное значение можно посмотреть в палитре «Свойства» (горячая клавиша Ctrl+1).
ПРИМЕЧАНИЕ: Преобразование единиц площади из мм2 в м2 можно осуществлять путем вызова быстрого калькулятора, нажав на соответствующую кнопку в поле «Площадь» (см. рис.). Сам принцип аналогичен вышеописанному.
рис.). Сам принцип аналогичен вышеописанному.
Площадь в Автокаде 2013 и 2015. Есть разница?
Существенные изменения программа претерпела, начиная с 2009 версии (читать подробнее про версии AutoCAD). Поэтому площадь в Автокаде 2012-2015 версии, так же, как и 2009-2010, определяется по одному и тому же принципу, описанному выше.
Как видите, простейшие расчеты в Автокаде выполняются автоматически, а их значения можно посмотреть в свойствах объекта. Теперь вы знаете, как определить площадь в Автокаде и преобразовать это значение в удобные для вас единицы измерения.
Сколько метров 1 сотка земли и как правильно рассчитать площадь земельного участка?
Сколько метров 1 сотка земли? Что можно разместить на маленьком участке? Этим вопросом задаются многие люди, которые собираются приобрести собственный участок. В данной статье вы найдете ответ на эти вопросы.
Что такое сотка земли: размер сотки и происхождение данного названия
Сотка — разговорное обозначение единицы меры площади, известной как «Ар». Используется в земледелии для обозначения площади земельного участка. Она представляет собой площадь квадрата со сторонами 10 на 10 метров. Слово ар происходит от латинского «ареаи», французского «are»(площадь, поверхность).
Используется в земледелии для обозначения площади земельного участка. Она представляет собой площадь квадрата со сторонами 10 на 10 метров. Слово ар происходит от латинского «ареаи», французского «are»(площадь, поверхность).
Впервые данная мера площади стала официальной во Франции в 1795 году. Название «сотка» связано с тем, что ар является сотой частью гектара или представляет собой площадь участка в 100 м2.
Перевод соток в другие единицы измерения площади
Кроме гектара, кратным по отношению к сотке является дунам, равный 10 соткам, который используется в странах Ближнего Востока. Сантиар, обозначающий площадь квадрата, стороны которого равны одному метру.
В нашей стране чаще всего используются следующие единицы измерения площади:
- Квадратный метр (1/100 сотки) – самая малая единица измерения площади;
- Сотка (100 м2) — квадрат со сторонами 10*10 м, именно в них измеряются садовые и приусадебные участки;
- Гектар (10 соток) – квадрат со сторонами 100*100 м, в них считается площадь сельскохозяйственных полей;
- Квадратный километр (10000 соток) – квадрат со сторонами 1000*1000 м, именно в км2 считается площадь земной поверхности.

Чему равна 1 сотка?
Данные единицы пришли в Россию после Революции 1917 года заменив старорусские меры площади, такие как:
- Квадратная верста – примерно 11000 соток;
- Десятина – примерно 11 соток;
- Четь – примерно 5 соток;
- Осьминник – примерно равный сотке.
Для чего нужны измерения земли?
Измерять площади своих участков люди стали ещё в древние времена, когда люди стали переходить на оседлый образ жизни.
С начала люди использовали субъективные единицы, например, в Древней Руси мерой площади был «плуг» — участок поля, который возможно перепахать на лошади за один день. Американские индейцы за единицу меры площади брали участок, который человек может обежать за день.
В Индии единицей меры площади был участок, на котором можно было разместить один загон для овец.
Существование различных мер веса, площади и длины в разных странах было очень неудобным. Это мешало развитию ремесел, торговли, и в 1791 году Национальное собрание Франции по предложению Комиссии по мерам и весам Академии наук установило новую систему мер, по этой системе вес измерялся в килограммах, длина — в метрах, а площадь участков земли — в арах.
Кто должен замерять участок перед оформлением и приватизацией?
Измерение площади земли называется «межеванием». Данное действие выполняют специально обученные люди – инженеры-геодезисты.
Когда требуется проведение межевания:
- При покупке земельного участка с неопределёнными границами;
- При объединении участков, расположенных рядом;
- При разделении одного большого ограждения на несколько мелких;
- Во время конфликта с соседями, по поводу незаконного захвата части чужой земли.
Но в некоторых случаях можно обойтись и без межевания:
- Если при покупке земли вы получили кадастровый паспорт данного объекта, то обновлять данный документ не требуется
- Когда владелец участка собирается оформить строение, расположенное на нём, достаточно наличие кадастрового паспорта, с планом участка в масштабе 1 к 500.
Чтобы получить кадастровый паспорт, нужно обратиться в Кадастровую палату со следующими документами:
- Заполненное заявление;
- Документ, подтверждающий право собственности на земельный участок;
- Копию паспорта владельца;
- Квитанцию об уплате госпошлины.

Вычисление площади участка правильной и неправильной формы
Для измерения площади участка правильной формы можно использовать даже то, что можно найти под ногами, например, палку. Если взять метровую палку и отмерить десять палок в ширину и десять в длину, то получится одна сотка. Можно повторить эту процедуру на всём несколько раз и узнать его площадь.
Также для измерения площади участка можно использовать рулетку, желательно десятиметровую. Повторяя такие же действия, как и с палкой, можно измерить площадь земли.
Для вычисления площади участка неправильной формы удобнее будет разделить его на разные геометрические фигуры и вычислить их площадь в квадратных метрах. Чтобы высчитать площадь фигуры, нужно перемножить длины её диагоналей, получившиеся число умножить на синус угла между диагоналями и после всё это разделить на два.
Чтобы вычислить площадь прямоугольного участка, нужно измерить его длины сторон(a, b, c, d), вычислить периметр (p) и подставить всё это в формулу: S=√(p-a)*(p-b)*(p-c)*(p-d).
Все данные, полученные в ходе измерений, будут занесены в кадастровый паспорт участка.
Чтобы измерить площадь земельного участка, который находится на склоне, геодезисты используют специальный прибор – нивелир. По центру участка ставится балка и прибор устанавливается в горизонтальной плоскости.
Что можно разместить на маленьком участке?
Конечно, многие люди хотят иметь привлекательный садовый участок, но необязательно он должен иметь большую площадь. Даже из маленького участка в 3-4 сотки можно сделать произведение искусства, пользуясь следующими советами.
- Можно визуально расширить участок, используя в его дизайне извилистые линии.
- В маленькие пространства очень хорошо вписываются подпорные стенки, которые можно оживить плетущимися растениями или даже овощными культурами, что будет выглядеть очень оригинально.
- Для посадки на небольшом участке лучше выбирать многолетние или вечнозелёные растения, которые никогда не будут портить внешний вид участка, оставаясь красивыми и аккуратными круглый год.

- Можно создавать игру формы растений, перемешивая пирамидальные с вертикальными и шаровидными.
- Для участков с маленькой площадью лучше выбирать один цветовой оттенок, ограниченная цветовая палитра также поможет создать эффект визуального расширения.
На маленьком участке также можно разместить и небольшой огород. Чтобы использовать его максимально эффективно можно использовать скороспелые растения и сажать дважды в один сезон. Также можно делать вертикальные грядки, которые отлично подойдут для томатов, огурцов и клубники, а картошку можно посадить в мешки. Используя подвесные мешки, можно разместить под ними контейнеры с другими культурами, тем-самым сэкономив полезное пространство.
В представленном ниже видео ролике вы можете видеть как можно спроектировать огород всего на одной сотке:
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Смотрите также Телефоны для консультации 13 Июл 2019 Юлия Юрьевна
538 Поделитесь записью
Как рассчитать площадь земли или участков неправильной формы
Если вы геодезист или владелец земли, на которой хотите рассчитать площадь земли, то вы попали в нужное место. У геодезиста или учащихся всегда возникают общие проблемы с определением площади неровной земли.
У геодезиста или учащихся всегда возникают общие проблемы с определением площади неровной земли.
Если земля квадратная, прямоугольная, треугольная, то мы можем легко найти площадь земли, используя простую геометрическую формулу. Обсудим, как по порядку посчитать площадь всех типов земель.
Все участки или земля не имеют фиксированной геометрической формы, такой как треугольник, прямоугольник или квадрат. Таким образом, нам часто приходится сталкиваться с трудностями при расчете площади таких земель, которые не имеют фиксированной геометрической формы.
Давайте опишем и разберем все возможные типы и формы земель, которые мы обычно должны вычислить.
1) Участки треугольной формы или земельный участок
Такие земли встречаются редко, но это не значит, что вам не придется сталкиваться с этой проблемой.Вы, вероятно, можете получить эти типы земли на углу края дороги или поворотной точке. Итак, давайте вкратце решим эти типы проблем.
Q) Рассчитайте площадь данного треугольного участка земли со стороной 21 м, 13 м и 20 м соответственно.

Решение: —
Пусть, Заданная сторона треугольника будет,
(AB) = (a) = 21 метр
(AC) = (b) = 21 метр
(AB) = (c) = 21 метр
У нас есть,
Итак, сначала рассчитаем полупериметры = (a + b + c) / 2 = (20 + 21 + 13) / 2 = 27 м.
Полупериметр треугольника равен половине его периметра, т. Е. (Сумма их сторон).
Теперь, используя приведенную выше формулу, мы получаем
Площадь треугольного участка земли (А)
Таким образом, мы можем рассчитать площадь земель треугольной формы. Теперь посчитаем площадь прямоугольных участков земли.
2) Участки прямоугольной формы или земельный участок
Эти типы земель часто встречаются во всех областях. Стороны земли, одна сторона которых равна их противоположной стороне, а другая сторона равна другой стороне, известны как прямоугольные земли.
Все стороны перпендикулярны друг другу, то есть под углом 90 градусов друг к другу. Давайте разберемся с помощью цифр и цифр, приведенных ниже.
Давайте разберемся с помощью цифр и цифр, приведенных ниже.
Q) Рассчитайте площадь прямоугольной площадки, размеры которой указаны на рисунке ниже.
Решение. Здесь на рисунке две стороны равны 14 метрам, а две стороны — 8 метрам.
Итак, пусть длина (L) = 14 метров и ширина (B) = 8 метров
У нас есть,
Итак, используя приведенную выше формулу, мы получаем
Площадь = L X B = (14 X 8) = 112 м 2
Таким образом, мы можем рассчитать площадь земельных участков прямоугольной формы.А теперь посчитаем площадь участков или земли.
Также читается,
что такое строка счетчика
Как проверить качество цемента на участке
Конструкция септика
3) Квадратные участки или земельный участок
Эти типы земель также распространены во всех областях. вы получите форму земли в основном и почти прямоугольной или квадратной формы. Стороны земли, все стороны которых равны друг другу, известны как квадратная земля.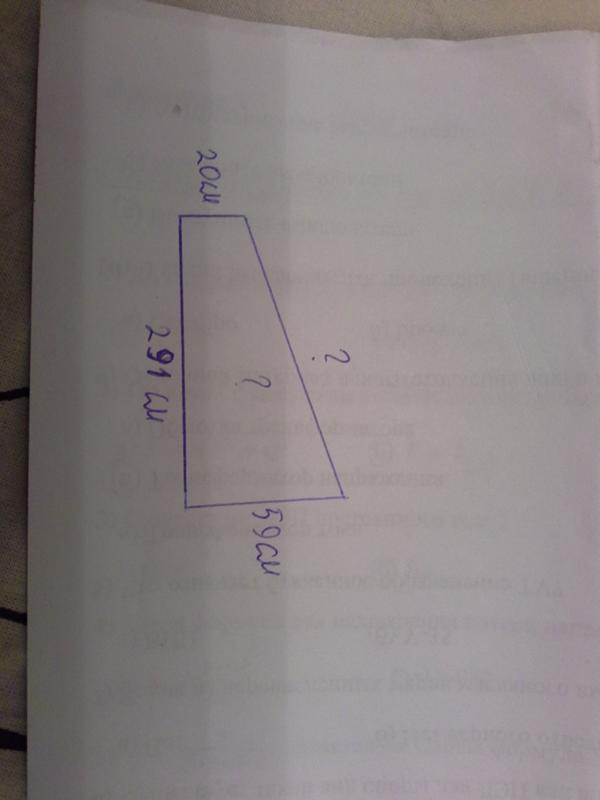
Все стороны перпендикулярны друг другу i.е 90 градусов друг с другом. Давайте разберемся с помощью цифр и цифр, приведенных ниже.
Q) Вычислите площадь квадратного участка земли, размеры которого указаны на рисунке ниже.
Решение, Здесь на рисунке все стороны равны и 8 метров.
итак, пусть длина (L) = 8 метров
У нас есть,
Используя формулу выше,
Площадь земли (A) = (8 X 8) м 2 = 64 м 2
Таким образом, мы можем вычислить площадь земли квадратной формы.А теперь посчитаем площадь приусадебных участков или земельных участков.
4) Трапеция земля
Этот тип земли может быть регулярным или неправильным. Я описываю здесь все типы земель на примерах. Давайте обсудим всю землю с помощью фигуры и формулы для ее расчета.
A) Участок с двумя параллельными друг другу сторонами
Эти типы земель находятся на обочине дороги и, возможно, искусственно созданы для других целей. В этом типе земли две стороны параллельны друг другу, а две другие — нет.Давайте разберемся на примере.
В этом типе земли две стороны параллельны друг другу, а две другие — нет.Давайте разберемся на примере.
Вы также можете рассчитать площадь вышеупомянутой земли, разделив землю на две части в прямоугольнике и треугольнике, которые вы можете увидеть на рисунке зеленой линией.
После этого вы можете снова использовать формулу квадрата и треугольника относительно друг друга и получить общую площадь.
Надеюсь, вы поняли и можете рассчитать площадь этих земель. Давайте посмотрим на другой тип неровной земли, который вы обычно находили при обследовании. но не волнуйтесь, я также произведу нумерацию этой земли.так что давайте двигаться вперед.
B) Участки, не имеющие параллельных друг другу сторон
Этот тип земли чаще всего встречается в любом месте штата и страны. Это неровная земля. В этих типах земель все стороны отличаются друг от друга. а также они составляют разные углы друг друга.
Геодезистам приходится рассчитывать эти типы земель, поэтому часто, и у них возникает больше проблем с такими типами земель, чтобы вычислить фактическую площадь. давайте разберемся с цифрами и формулой для расчета площади земли.
давайте разберемся с цифрами и формулой для расчета площади земли.
Q) Рассчитайте площадь неровной земли, размер которой указан на рисунке ниже.
Решение,
Рассчитать эти типы земель очень просто. Чтобы узнать площадь этих типов земель, в первую очередь закопайте четыре колышка или дальномер на всех углах участка. После этого сделайте замеры со всех сторон земли. и имейте в виду, что вы должны измерить любую диагональ участков.
Теперь, как вы можете видеть на рисунке, вся территория разделена на две части с синими диагоналями линий, и они имеют форму треугольника.
Вот и все, используйте формулу треугольной земли отдельно и сложите обе, чтобы получить общую площадь. разве это не легко?
А теперь перейдем к расчету,
В треугольнике ABD,
let, BD (a) = 5 метров, AD (b) = 3 метра, AB (c) = 4 метра
Снова имеем
где S = (5 + 3 + 4) / 2 = 6 метров.
Итак, складывая все значения, получаем Площадь треугольника ABD = 6 м 2
Аналогично для треугольника BDC,
let, DC (a) = 13 метров, BC (b) = 12 метров, BD (c) = 5 метров
где (S) = (13 + 12 + 5) / 2 = 15 метров.
Итак, подставив все значения, получаем Площадь треугольника BDC = 30 м 2
Таким образом, общая площадь земли стала,
= Площадь треугольника ABD и треугольника BDC
= (6 + 30) м 2
= 36 м 2
Таким образом, мы можем вычислить площадь земли неправильной формы.
Итак, ребята, я надеюсь, что эта статья « как рассчитать площадь » останется для вас полезной.Пожалуйста, поделитесь им и продолжайте посещать, чтобы получать ежедневные обновления.
Загрузите лист Excel здесь,
Просмотры сообщений:
4 038
Связанное сообщение
Площадь земельного участка — Доктора математики
Последние четыре сообщения были посвящены формулам для поиска областей с использованием длин сторон, начиная с треугольника, где это все, что вам нужно, а затем с четырехугольников, где нужно добавить что-то еще; а затем используя координаты вершин. Теперь мы можем использовать эти инструменты для решения некоторых из наиболее распространенных реальных проблем, которые мы получили: определение площади земельного участка. Будет несколько методов, в зависимости от того, какие данные у вас есть помимо длины.
Теперь мы можем использовать эти инструменты для решения некоторых из наиболее распространенных реальных проблем, которые мы получили: определение площади земельного участка. Будет несколько методов, в зависимости от того, какие данные у вас есть помимо длины.
Четыре стороны и диагональ
Вот вопрос от 2002 года:
Площадь газона У меня есть два участка газона, которые я хочу засыпать новой травой, и я не знаю, сколько газона купить. Один газон имеет ширину 14 ярдов на одном конце и 7 ярдов на другом конце .Длина составляет 16 ярдов и 20 ярдов . Другой газон 30 ярдов в длину, 32 ярда в длину, 5 ярдов в ширину и 10 ярдов в ширину. Дерн бывает квадратами. Я легко могу срезать дерн лопатой. Позвольте мне попытаться лучше описать газон (и). Если нарисовать на бумаге следующее. Верхняя часть лужайки 14 ярдов в поперечнике. Нижняя сторона имеет ширину 7 ярдов. Левая сторона проходит 16 ярдов, а правая проходит 22 ярда.На бумаге диагональ от верхнего правого угла до нижнего левого угла составляет примерно 20 ярдов. От верхнего левого угла до нижнего правого угла примерно 22 ярда. На другом газоне ширина его вершины составляет 10 ярдов. Нижняя сторона 5 ярдов в поперечнике. Левая сторона составляет 30 ярдов, а правая - 32 ярда. Диагональ от верхнего правого угла до нижнего левого угла составляет примерно 31 ярд. От верхнего левого угла до нижнего правого примерно 33 ярда.
Первоначального описания, дающего только «длину» и «ширину» (как если бы это был прямоугольник), было недостаточно; но Рэнди мудро дал нам именно то, о чем мы просили других: длину диагоналей тоже.Это дает возможность сделать чертеж в масштабе; вот как выглядит первое:
Обратите внимание, что если диагональ BD составляет ровно 20 ярдов, AC — не совсем 22. Оба они были описаны как приблизительные, так что это лучшее, что мы можем сделать. Цифра «завышена» с небольшим противоречием между числами; но тот факт, что это так близко, вселяет уверенность в том, что все числа достаточно точны.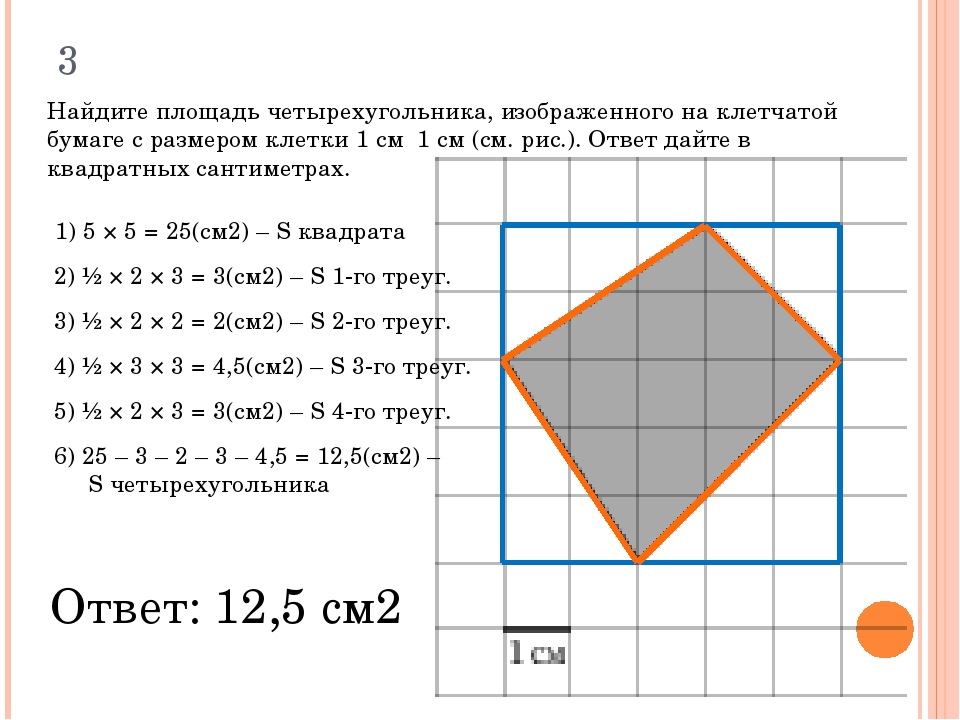 Мы найдем такое подтверждение полезным во многих задачах подобного типа.
Мы найдем такое подтверждение полезным во многих задачах подобного типа.
Доктор Иеремия ответил, впервые представив формулу Герона, которую мы видели раньше:
Давайте посчитаем площадь, а после мы можем посчитать количество квадратов.Площадь треугольника можно найти так:
Предположим, что газон можно разрезать по диагонали, чтобы получился треугольник. Затем мы можем использовать формулу Герона, чтобы найти площадь
+ ----------------- а ----------------- +
\ +
\ +
\ +
\ +
до н.э
\ +
\ +
\ +
+
Сначала вычислите промежуточное значение: s = (a + b + c) / 2 Тогда площадь равна: Area = sqrt [s (s-a) (s-b) (s-c)], где sqrt [x] - квадратный корень из x.
Поскольку любая диагональ делит многоугольник на два треугольника, нам просто нужно применить это дважды. Во-первых, мой ABD:
Итак, для вашего первого газона мы будем работать с верхним левым треугольником, а затем с нижним правым треугольником.Высота лужайки составляет 14 ярдов (назовите это значение «а»). Левая сторона составляет 16 ярдов (назовите это значение «b»). Третья сторона треугольника - диагональ. Диагональ от верхнего правого угла до нижнего левого угла
составляет примерно 20 ярдов (назовите это 'c').Тогда s = (a + b + c) / 2 = (14 + 16 + 20) / 2 = 50/2 = 25 квадратных ярдов, а площадь этого треугольника равна sqrt [s (sa) (sb) (sc)] . Если мы подключим a, b, c и s, мы получим: sqrt [s (s-a) (s-b) (s-c)] sqrt [25 (25-14) (25-16) (25-20)] sqrt [25 (11) (9) (5)] sqrt [12375] Площадь верхнего левого треугольника: 111,24 кв. ярда
Далее мой BCD:
Теперь создадим другой треугольник, составляющий лужайку: Нижняя сторона - 7 ярдов в поперечнике (назовите это «а»). Правая сторона проходит 22 ярда (назовите это «b»). Диагональ от верхнего правого угла до нижнего левого угла
составляет примерно 20 ярдов (это «с»).Тогда s = (a + b + c) / 2 = (7 + 22 + 20) / 2 = 49/2 = 24,5 квадратных ярда, а площадь этого треугольника равна sqrt [s (sa) (sb) (sc) ].Если мы подключим a, b, c и s, мы получим: sqrt [s (s-a) (s-b) (s-c)] sqrt [24,5 (24,5-7) (24,5-22) (24,5-20)] sqrt [24,5 (17,5) (2,5) (4,5)] sqrt [4823.4375] Площадь нижнего правого треугольника: 69,45 кв. ярда Это означает, что общая площадь лужайки равна сумме двух треугольных площадей, в общей сложности 180,69 квадратных ярдов. Если 1 квадрат дерна равен 1 квадратному ярду, то вам понадобится 181 квадрат дерна (потому что вы не можете купить 0.69 квадратов дерна).
Можно использовать и другую диагональ. Вот моя работа для этого с использованием указанных Рэнди 22 ярдов, что означает, что площадь, вероятно, будет немного другой:
$$ K_ {ABC} = \ sqrt {(29) (15) (7) (7)} = \ sqrt {21315} = 146,00; $$
$$ K_ {ACD} = \ sqrt {(22,5) (6.5) (15.5) (0.5)} = \ sqrt {1133.44} = 33,67; $$
$$ K_ {ABCD} = K_ {ABC} + K_ {ACD} = 179,67. $$
Это отличается от других расчетов всего на 1 квадратный ярд, что хорошо.
Другой газон будет сделан таким же образом.И вообще, площадь чего угодно можно вычислить, если разбить ее на треугольники.
Вот изображение:
Опять же, вторая диагональ, BD, не совсем совпадает, но ее достаточно. Я оставлю это на ваше усмотрение. (GeoGebra дает площадь как 222,56, если вы хотите проверить.)
Похожий метод (с дополнительными идеями для расчета углов) можно найти здесь:
Ковровое покрытие неправильного шестиугольника
Четыре стороны и один (прямой) угол
Рассмотрим этот вопрос из 2003:
Определение площади участка землиУ меня есть участок земли, площадь которого мы пытаемся вычислить.Существуют различные записи, которые показывают разные результаты, но следующая - лучшая запись, которая у меня есть по размерам. Не могли бы вы дать ответ и формулу? Размеры: 98,20 x 100,89 x 140,79 x 0,89 футов
Гэри указал только длины сторон, что, как мы знаем, недостаточно. Но только что нарисовав его, я понял, что одна сторона намного короче других, что сделало его практически треугольником. Если бы нам не нужна была точность, мы могли бы просто применить формулу Герона к сторонам 98.20 ′, 100,89 ′ и 140,79 ′: У нас есть \ (s = 169.94 \), поэтому $$ K = \ sqrt {(169.94) (71.74) (69.05) (29.15)} = \ sqrt {24539133.78} = 4953,7.
Если бы нам не нужна была точность, мы могли бы просто применить формулу Герона к сторонам 98.20 ′, 100,89 ′ и 140,79 ′: У нас есть \ (s = 169.94 \), поэтому $$ K = \ sqrt {(169.94) (71.74) (69.05) (29.15)} = \ sqrt {24539133.78} = 4953,7.
$
Доктор Роб ответил на вопрос:
Вы не предоставили достаточно информации для решения проблемы. Лучшее, что я могу вам сказать, это то, что площадь * не более * 5016,35 квадратных футов. Чтобы точно ответить на ваш вопрос, вам нужно будет указать хотя бы один из углов, или диагональное расстояние, или некоторые дополнительные данные. Например, параллельны ли две стороны? Область выпуклая?
...
Оказывается, максимальная площадь достигается, когда четыре угла участка лежат на окружности одного круга. Вот как я мог вычислить максимальную площадь вашей задачи.
Он нашел максимально возможную площадь, используя формулу Брахмагупты для циклического четырехугольника: $$ s = (98,20 + 100,89 + 140,79 + 0,89) \ div 2 = 170,385 \\ K = \ sqrt {(sa) (sb) (sc) ( sd)} \\ = \ sqrt {(72,185) (69,495) (29,595) (169,495)} \\ = \ sqrt {25163772,82} = 5016,35. $$
$$
Гэри ответил углом:
Спасибо, что нашли время ответить.У меня есть один угол в 90 градусов на пересечении сторон размером 98,20 x 100,89 дюйма.
Этого одного угла достаточно (и, фактически, любая конфигурация этих сторон будет там очень близка к прямому углу).
Доктор Роб теперь мог ответить на вопрос, найдя площадь прямоугольного треугольника, а затем используя его гипотенузу в формуле Герона для другого (очень тонкого) треугольника:
Спасибо, что ответили Ask Dr. Math, Gary.
Хорошо! Прямоугольный треугольник, образованный в этом углу путем рисования другой диагонали, имеет гипотенузу длины.
L = sqrt (98.2) = 140,79073 ... футов.
Тогда площадь прямоугольного треугольника равна
A1 = (1/2) * b * h,
= 0,5 * 100,89 * 98,20,
= 4953,699 квадратных футов,
а площадь другого треугольника, используя формулу Герона, равна
A2 = sqrt [s * (s-a) * (s-b) * (s-c)],
где
a = 140,79073 футов,
b = 140,79 футов,
c = 0,89 футов,
s = (a + b + c) / 2 = 141,235365 футов,
так
A2 = sqrt (141,235365 * 0,444635 * 0,445365 * 140,345365),
= sqrt (3925. 195215 ...),
= 62,651378 ... квадратных футов.
Тогда сумма будет
А = А1 + А2 = 5016.350378 ... квадратных футов,
что равняется максимально возможному значению 5016.35054787 ... до трех десятичных знаков (но не точно).
Не стесняйтесь писать еще раз, если я могу еще помочь.
195215 ...),
= 62,651378 ... квадратных футов.
Тогда сумма будет
А = А1 + А2 = 5016.350378 ... квадратных футов,
что равняется максимально возможному значению 5016.35054787 ... до трех десятичных знаков (но не точно).
Не стесняйтесь писать еще раз, если я могу еще помочь. Если бы один известный угол отличался от 90 градусов, мы могли бы использовать тригонометрию, чтобы найти площадь и стороны первого треугольника, так что это иллюстрирует более общий метод.
Доктор Кен описывает чисто тригонометрический метод с использованием углов:
Площадь неправильного многоугольника
Два угла к каждой вершине
Геодезисты, как мы знаем из наблюдений за их работой, сосредотачиваются на поиске углов, а не расстояний.Следующий вопрос от 1999 года о том, как это работает:
Площадь многоугольникаЯ обнаружил, что в популярной небольшой книге по математике в мягкой обложке сказано, что геодезист может вычислить площадь многоугольника следующим образом: 1.
Проложите и измерьте линию любой длины
внутри многоугольника («базовая линия»). 2. Измерьте угол к каждой вершине многоугольника
от каждого конца линии . Результирующая длина единственной линии и углы предположительно содержат достаточно информации для вычисления площади.Пытаясь решить эту проблему, я смог вычислить площади треугольников, одна из сторон которых является базовой линией, и мне удалось решить некоторые, но не все, другие треугольники. Я застрял на нескольких периферийных треугольниках, для решения которых я не могу получить достаточно информации. Есть ли общий алгоритм решения этой проблемы для многоугольников с любым количеством сторон; выпуклые, вогнутые или когда у вас нет длин сторон? Если я когда-нибудь смогу это понять, я хочу написать программу для выполнения вычислений.
Есть несколько способов сделать это; Принимая во внимание тот факт, что формула шнурков, которую я обсуждал в прошлый раз, также называется формулой геодезиста, я предложил способ использования тригонометрии для поиска координат, которые можно вставить в эту формулу:
Очевидно, что в углах и базовой линии достаточно информации, потому что их достаточно, чтобы нарисовать фигуру (многократно используя ASA), и поэтому площадь определяется этими числами.Вы, конечно же, хотите знать КАК? Я не знаком ни с одним традиционным методом, используемым геодезистами, но я, по крайней мере, могу придумать метод, который будет работать.Требуется два шага. Во-первых, если мы выберем систему координат, в которой один конец базовой линии является началом, а другой - точкой (d, 0), мы можем найти координаты каждой вершины. Я использовал эту цифру: п + / | \ / | \ / | \ / | у \ / | \ / | \ / а | б \ + ------- + --------------- + А х г-х Б написать два уравнения у / х = загар (а) у / (д-х) = загар (б) из которых я получил формулы д д x = ---------- и y = --------------- загар (а) 1 1 ------ + 1 ------ + ------ загар (б) загар (а) загар (б) Вы можете проверить их; Я сделал это довольно быстро, но это дает представление.Случаи, когда касательные равны нулю или бесконечны, обрабатываются легко.
Второй шаг - использовать эти координаты для каждой точки (x_n, y_n), чтобы найти область.
Для этого есть стандартная формула: A = [(x1y2 + x2y3 + ... + xny1) - (y1x2 + y2x3 + ... + ynx1)] / 2 Я думаю, этого должно быть достаточно - может быть, не так элегантно, как могло бы быть, но довольно просто.
Поскольку здесь нет конкретных цифр, давайте приведем пример. Я нарисовал пятиугольник и измерил углы от каждого конца стороны AB до других вершин C, D и E:
Наша базовая линия составляет 5 метров; мы можем взять точку A как (0, 0), а B как (5, 0).Для точки C углы составляют 23,2 ° и 123,69 °, поэтому мы находим $$ x = \ frac {d} {\ frac {\ tan \ alpha} {\ tan \ beta} + 1} = \ frac {5} { \ frac {\ tan 23.2 °} {\ tan 123.69 °} + 1} = \ frac {5} {\ frac {0.4286} {- 1.5000} + 1} = 7.000 $$ $$ y = \ frac {d} { \ frac {1} {\ tan \ alpha} + \ frac {1} {\ tan \ beta}} = \ frac {5} {\ frac {1} {\ tan 23,2 °} + \ frac {1} {123,69 °}} = \ frac {5} {\ frac {1} {0.4286} + \ frac {1} {- 1.5000}} = 3.000. $$ (Да, я выбрал свои точки с простыми координатами, в отличие от реальной жизни.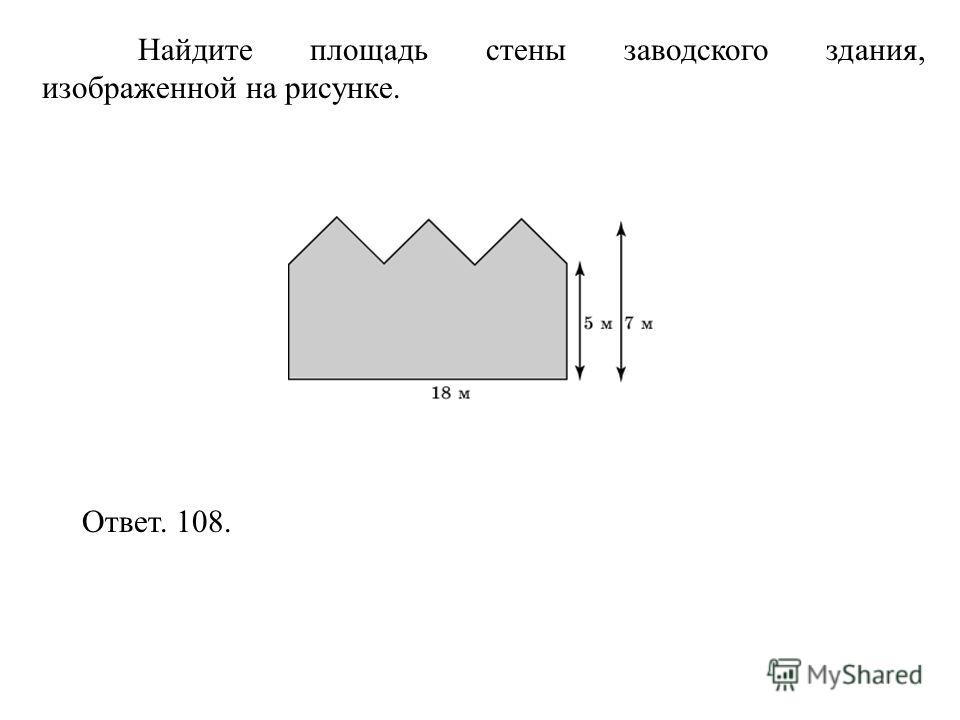 ) Итак, C — это (7, 3). Точно так же D — это (1, 5), а E — (-1, 2). Используя формулу шнурков, мы помещаем пять упорядоченных пар в массив (первая из которых скопирована внизу), $$ \ begin {bmatrix} 0 & 0 \\ 5 & 0 \\ 7 & 3 \\ 1 & 5 \ \ -1 & 2 \\ 0 & 0 \ end {bmatrix} $$
) Итак, C — это (7, 3). Точно так же D — это (1, 5), а E — (-1, 2). Используя формулу шнурков, мы помещаем пять упорядоченных пар в массив (первая из которых скопирована внизу), $$ \ begin {bmatrix} 0 & 0 \\ 5 & 0 \\ 7 & 3 \\ 1 & 5 \ \ -1 & 2 \\ 0 & 0 \ end {bmatrix} $$
Тогда наша площадь равна $$ K = \ frac {1} {2} [(0 + 15 + 35 + 2 + 0) — (0 + 0 + 3-5 + 0)] = 27 \ text {квадратных метров.} $$
Данные съемки: длины и направления
Мы рассмотрим еще один тип ввода: фактические геодезисты наносят так называемую платформенную карту.
Земельный участок, площадьУ меня есть земельный участок трапециевидной формы. Четыре стороны не равны. Фасад дороги составляет 363,04 фута в северо-восточном направлении. Одна сторона - 1950,16 футов в юго-восточном направлении. Спина 338,49 футов в юго-западном направлении. Последняя сторона находится на высоте 2000,75 футов в северо-западном направлении.Инспектор определил, что площадь составляет 624 630,88 квадратных футов, а общая площадь составляет 14 340 акров.
Юридическое описание составляет 15,8 акров. Как я могу определить площадь в квадратных футах?
Вот четыре длины и общие направления — близкие к тому, что нам нужно.
Я ответил:
Вы называете это трапецией, но я подозреваю, что вы не имеете в виду, что две стороны строго параллельны, иначе вы, вероятно, так сказали бы. Не зная хотя бы одного точного угла (лучше, чем «северо-восток»), я не могу найти точную область.Вы знаете подшипники с каждой стороны? Данные квадратные футы конвертируются в 14,340 акров; и 15,8 акров - это очень близко к тому, что вы получите, просто умножив среднюю «длину» на среднюю «ширину», что может свидетельствовать о том, что площадь изначально была найдена упрощенным и неточным методом, или это может быть правильным, если углы равны в самый раз. Пожалуйста, пришлите мне данные о ракурсе, и я дам вам лучший ответ.
Том ответил (как мало кто когда-либо делал) со всеми данными:
Углы и размеры, указанные на платформе, следующие: 363.04 фут - с.ш.38 град. 15 '00 "в.д. 1950,16 ft - на платформе написано: S 80 deg 36 '34 "E. 338,47 футов - на платформе указано: S 30 градусов 59 '49 дюймов з.д. 200.75 пт - N 80 град 42 '11 "з.д. Надеюсь это поможет; это все, что есть на планшете.
Для каждой стороны у нас есть не только длина, но и направление. Обозначение, если вы не знакомы с ним, означает следующее:
- N 38 ° 15 ′ 00 ″ E означает начало направления на север и поворот на восток на 38 градусов, 15 минут и 00 секунд
Поскольку это был такой хороший пример, я подробно описал свою работу для будущего использования (а также сделал электронную таблицу, которая много раз использовалась для такого рода вопросов и с годами улучшалась).
Хорошо, давайте сначала конвертируем углы из терминов геодезистов в мои. Я измерю углы по часовой стрелке от севера и представлю их в десятичной форме (форма «N x E» означает, что мы начинаем с севера и идем на x градусов к востоку):
AB: N 38 ° 15 '00 "E -> 38,25 °
BC: ю. ш. 80 град. 36 '34 "в.д. -> 180–80,61 = 99,391 град.
CD: ю. Ш. 30 град. 59 '49 "з. Д. -> 180 + 30,997 = 210,997 град.
DA: с.ш. 80 град. 42 '11 "з.д. -> 360–80,703 = 279,297 град.
Это должно выглядеть примерно так
B ----_____ 1950
363 / -----_____
/ ---- С
A ----_____ /
-----_____ / 338
2000 ---- D
ш. 80 град. 36 '34 "в.д. -> 180–80,61 = 99,391 град.
CD: ю. Ш. 30 град. 59 '49 "з. Д. -> 180 + 30,997 = 210,997 град.
DA: с.ш. 80 град. 42 '11 "з.д. -> 360–80,703 = 279,297 град.
Это должно выглядеть примерно так
B ----_____ 1950
363 / -----_____
/ ---- С
A ----_____ /
-----_____ / 338
2000 ---- D Вот вариант рисунка на GeoGebra:
Теперь мы можем превратить каждую сторону в вектор, указав, как далеко она проходит N и E; северный компонент - это L cos (A), где L - длина стороны, A - угол с севера, а восточный компонент - это L sin (A).Угол длины стороны Северо-восток
---- ------ ----- ----- ----
AB 363.04 38.250 285.101 224.756
До н.э. 1950,16 99,391 -318,195 1924,026
КД 338,47 210,997 -290,135 -174,309
DA 2000.75 279.297 323.224 -1974.469 Например, чтобы добраться из пункта А в пункт Б, мы идем на 285 футов к северу и 224 фута к востоку.
Теперь мы вызываем A (0, 0) и складываем, чтобы найти координаты каждой точки (которую я почему-то написал как север, y , а затем восток, x ).
Отсюда мы можем найти координаты каждой вершины относительно A:
К северо-востоку
----- ----
А 0 0
В 285.101 224.756
С -33.094 2148.782
Д -323.229 1974.473
(А) -.005 .004
Я включил место, куда мы вернемся, когда подойдем к точке А, чтобы проверить точность расчетов, и оно выглядит довольно неплохо. Если бы окончательные координаты не были близки к нулю, мы бы знали, что некоторые измерения были неправильными, потому что фигура не закрывалась бы.Это преимущество наличия большего количества информации, чем 5 или 6 фактов, необходимых для четырехугольника.
Наконец, имея координаты каждой вершины, я могу использовать формулу геодезиста (формула шнурков):
Теперь последний шаг - найти площадь, используя эту формулу из нашего FAQ по аналитической геометрии:
http://mathforum.org/dr.math/faq/formulas/faq.ag2.html#twopolygons
К = [(x1y2 + x2y3 + x3y4 + ... + xny1) -
(x2y1 + x3y2 + x4y3 + .. . + x1yn)] / 2
Это делает область
К = [(0 * 224.2 на акр, дает 14,34 акра.
Неудивительно, что геодезист, похоже, правильно использовал свои собственные данные.
. + x1yn)] / 2
Это делает область
К = [(0 * 224.2 на акр, дает 14,34 акра.
Неудивительно, что геодезист, похоже, правильно использовал свои собственные данные. Подобный метод описан здесь доктором Джерри:
Расчет площади многоугольника
5. РАСЧЕТ ПОВЕРХНОСТИ ПОЛЕЙ НЕРЕГУЛЯРНОЙ ФОРМЫ
5. РАСЧЕТ ПОВЕРХНОСТИ ПОЛЕЙ НЕРЕГУЛЯРНОЙ ФОРМЫ
5.1 Пример 1
5.2 Пример 2
Распространенной проблемой для геодезистов является расчет площади поверхности
поле фермера.Поля часто нерегулярны, что требует прямого расчета.
из их районов сложно. В таком случае поля делятся на ряд обычных
области (треугольники, прямоугольники и т. д.), из которых можно рассчитать поверхности
с простыми формулами. Все площади рассчитываются отдельно, и их сумма
area дает общую площадь поля.
На рисунке 29 показано поле неправильной формы, площадь поверхности которого необходимо определить.
Фиг.29 Поле неправильной формы
Следующая процедура:
Шаг 1
Сделайте грубый набросок поля (см. Рис. 29a), обозначив углы поля (A, B, C, D и E) и границы поля (прямые линии). Вдобавок какая-то главная достопримечательность! обозначены (дороги, канавы, дома, деревья и т. д.), которые могут помочь определить местонахождение поля.
Рис. 29a Черновой набросок поля
Шаг 2
Разделите поле, как показано на эскизе, на области правильной формы.В этом примере поле можно разделить на 3 треугольника ABC (основание AC и высота BB), AEC (основание AC и высота EE 1 ) и CDE (основание EC и высота DD 1 ) (см. Рис. 29b. ).
Рис. 29b Разделение поля на области правильной формы
Шаг 3
Отметьте на поле углы A, B, C, D и E колышками.
Шаг 4
Разместите вехи для измерения дальности на линиях AC (основание треугольников ABC и AEC) и EC (основание треугольника EDC) (см. Рис.29c) и измерьте расстояния AC и EC.
Рис.29c) и измерьте расстояния AC и EC.
Рис. 29c Отметьте углы колышками и разложите опоры для измерения дальности
Шаг 5
Проведите линию BB (высота треугольника ABC) перпендикулярно базовой линии AC (см. Рис. 29d), используя один из методов, описанных в главе 4. Измерьте расстояние BB,
Рис. 29d Проведите линию BB перпендикулярно к AC
Шаг 6
Таким же образом устанавливаются и измеряются высота EE треугольника AEC и высота DD треугольника CDE (см.рис.29e)
Рис. 29e Проведите линию DD 1 перпендикулярно к EC и линию EE1 перпендикулярно AC
Шаг 7
Основание и высота трех треугольников были измерены. Окончательный расчет можно произвести следующим образом:
Измерено
Треугольник ABC: основание = AC = 130 м
высота = BB 1 = 55 м
Треугольник ACE: основание = AC = 130 м
высота = EE 1 = 37 м
Треугольник CDE: основание = EC = 56 м
высота = DD 1 = 55 м
Ответ
Площадь = 0,5 x основание x высота
= 0.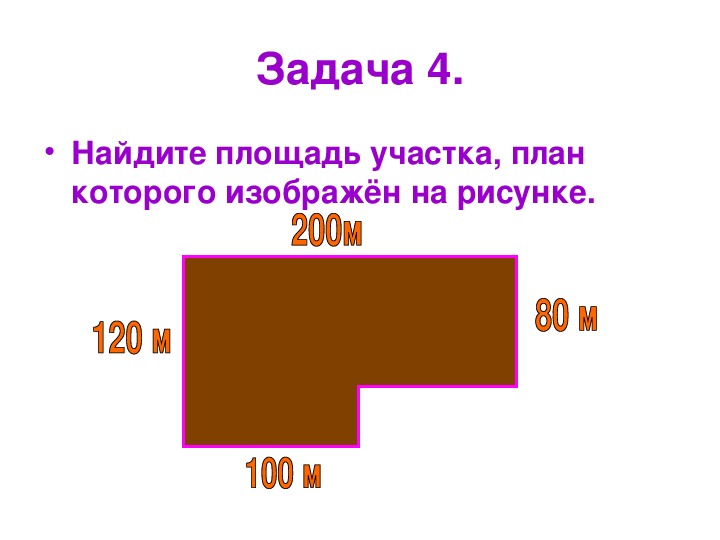 5 x 130 м x 55 м = 3 575 м 2
5 x 130 м x 55 м = 3 575 м 2
Площадь = 0,5 x 130 м x 37 м = 2 405 м
Площадь = 0,5 м x 56 м x 55 м = 1 540 м²
Поле ABCDE:
Площадь треугольника ABC = 3 575 м 2
Площадь треугольника ACE = 2405 м 2
Площадь треугольника CDE = 1540 м 2
Общая площадь = 3 575 м 2 + 2 405 м 2 + 1540 м 2
= 7 520 м- = 0,752 га
Площадь поверхности поля, показанного на рис.30 необходимо определять в то время, когда поле покрыто высокими культурами (например, кукурузой или сахарным тростником).
Рис.30 Поле, покрытое высоким урожаем
Поле можно разделить на два треугольника ABD и BCD (см. Рис. 31a). К сожалению, из-за высокого урожая невозможно установить и измерить базовый BD и две высоты AA 1 и CC 1 .
Рис. 31a Разделение поля на два треугольника
В этом случае площадь треугольника ABD может быть рассчитана с использованием AD в качестве основания и BB 1 в качестве соответствующей высоты.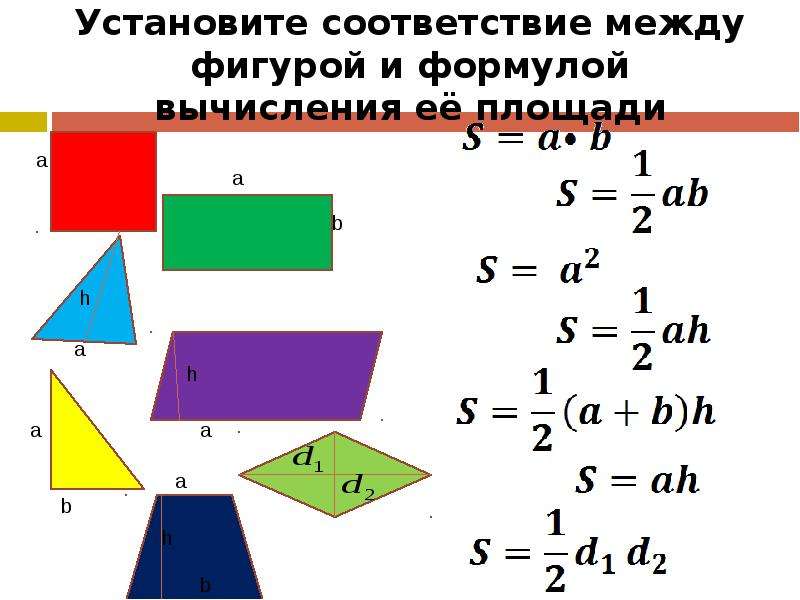 BB 1 можно установить и измерить за пределами посевной площади. Таким же образом можно рассчитать треугольник BCD, используя основание BC и соответствующую высоту DD 1 (см. Рис. 31b).
BB 1 можно установить и измерить за пределами посевной площади. Таким же образом можно рассчитать треугольник BCD, используя основание BC и соответствующую высоту DD 1 (см. Рис. 31b).
Рис. 31b Определение площадей двух треугольников
Порядок действий в поле:
Шаг 1
Отметьте 4 угла (A, B, C и D) с помощью опорных стоек.
Шаг 2
Линия AD обозначена мачтами и простирается за A.Линия BC также проходит и продолжается за C (см. Рис. 32a). Измерьте расстояния AD (основание треугольника ADB) и BC (основание треугольника BCD).
Рис. 32a Измерение оснований двух треугольников
Шаг 3
Проведите линию BB 1 (высота треугольника ABD) перпендикулярно расширенной базовой линии AD, используя один из методов, описанных в главе 4. Таким же образом устанавливается линия DD 1 (высота треугольника BCD). перпендикулярно удлиненной базовой линии BC (см. рис.32b) Измерьте расстояние BB 1 и DD 1 .
Рис. 32b Измерение высоты двух треугольников
Шаг 4
Основание и высота обоих треугольников были измерены. Окончательные расчеты можно произвести следующим образом:
Измерено
Треугольник ABD: основание = AD = 90 м
высота = BB 1 — 37 м
Треугольник BCD: основание = BC = 70 м
высота = DD 1 -50 м
Ответ
Площадь = 0.5 x основание x высота
= 0,5 x 90 м x 37 м = 1665 м 2
Площадь = 0,5 x 70 м x 50 м = 1750 м 2
Поле ABDC:
Треугольник площади ABD = 1 665 м²
Треугольник площади BCD = 1 750 м 2
Общая площадь = 1 665 м 2 + 1 750 м 2 = 3415 м 2
= 0,3415 га = ок. 0,34 га
Что такое площадь неправильной формы?
Участок неправильной формы
Неправильные формы — это многоугольники с пятью или более сторонами различной длины.Эти формы или фигуры можно разложить на треугольники, квадраты и четырехугольники для оценки площади.
Вот некоторые примеры неправильной формы:
Предметы повседневного быта неправильной формы
Расчет площади неправильной формы:
Подходы к оценке площади неправильной формы:
Оценка площади с использованием единичных квадратов
Примените эту технику для фигур с кривыми, кроме идеального круга или полукругов и неправильных четырехугольников.В этом методе разделите фигуру на единичные квадраты. Общее количество единичных квадратов, попадающих в форму, определяет общую площадь.
Рисунок: Некоторые примеры неправильной формы
Считайте квадрат как «1», если заштрихованная область покрывает более половины при вычислении площади для более точной оценки.
Рис.: Для фигур неправильной формы считайте квадраты с оранжевой и желтой кодировкой как 1.
На следующем рисунке рассчитайте площадь, подсчитав единичные квадраты, что составляет 6.Если обозначить каждую единицу квадрата в сантиметрах, то площадь будет 6 см2.
Рис.: Расчет площади неправильной формы с изогнутыми краями
- Разделение неправильной формы на две или более правильных формы
Используйте этот метод для неправильных форм, которые представляют собой комбинацию треугольников и многоугольников. Используйте стандартные формулы, чтобы вычислить площадь таких фигур и сложить их вместе, чтобы получить общую площадь.
Например, у неправильной формы мы разделяем несколько ребер на треугольник и три многоугольника.
Общая площадь фигуры определяется как:
⇒ Площадь = Площадь (ABIM) + Площадь (BCGH) + Площадь (CDEF) + Площадь (JKL)
⇒ Площадь = (AB × BI) + (BC × CG) + (CD × DE) + ( 1 ⁄ 2 × LJ × KO)
⇒ Площадь = (10 × 5) + (3 × 3) + (2 × 2) + ( 1 ⁄ 2 × 4 × 4)
⇒ Площадь = 50 + 9 + 4 + 8
⇒ Площадь = 71 см2
- Разделение неправильной формы кривыми на две или более правильных формы
В этом методе разложите неправильную форму на несколько квадратов, треугольников или других четырехугольников.В зависимости от формы и кривых, часть фигуры может быть кругом, полукругом или квадрантом.
На следующем рисунке изображена неправильная форма с 8 сторонами, включая одну кривую. Определите неизвестные величины по заданным размерам сторон. Разложите фигуру на два прямоугольника и полукруг.
Площадь фигуры ABCDEF составляет:
Площадь (ABCDEF) = Площадь (ABCG) + Площадь (GDEF) + Площадь (aob)
Площадь = (AB × AG) + (GD × DE) + ( 1 ⁄ 2 × π × ob2)
Площадь = (3 × 4) + (10 × 4) + ( 1 ⁄ 2 × 3.14 × 12)
Площадь = 12 + 40 + 1,57
Площадь = 53,57 см2
Приложение
Оценка площади неправильных фигур — важный метод для рисования карт, построения архитектуры и разметки сельскохозяйственных полей. Применяем концепцию кроя тканей по заданному дизайну. В старших классах эта техника закладывает основу для продвинутых тем, таких как вычисление объема, рисование конических сечений и фигур эллиптической формы.
Интересный факт |
Сопутствующий математический словарь
- Квадрат
- прямоугольник
- Треугольник
- Круг
- Площадь
- Неправильные и правильные формы
Калькулятор площади.Найдите область из 16 популярных фигур!
Если вам интересно, как рассчитать площадь любой основной формы, вы попали в нужное место — этот калькулятор площади ответит на все ваши вопросы. Воспользуйтесь нашим интуитивно понятным инструментом, чтобы выбрать из шестнадцати различных форм и вычислить их площадь в мгновение ока. Если вы ищете определение площади или, например, формулу ромба, у нас есть все необходимое. Продолжайте прокручивать, чтобы узнать больше, или просто поиграйте с нашим инструментом — вы не будете разочарованы!
Что такое площадь в математике? Определение площади
Проще говоря, площадь — это размер поверхности .Другими словами, его можно определить как пространство, занимаемое плоской формой. Чтобы понять концепцию, обычно полезно думать о площади как о количестве краски, необходимом для покрытия поверхности . Посмотрите на картинку ниже — все фигуры имеют одинаковую площадь, 12 квадратных единиц:
Есть много полезных формул для вычисления площади простых форм. В разделах ниже вы найдете не только хорошо известные формулы для треугольников, прямоугольников и кругов, но и другие формы, такие как параллелограммы, воздушные змеи или кольца.
Мы надеемся, что после этого объяснения у вас не возникнет проблем с определением области в математике!
Как рассчитать площадь?
Ну конечно это зависит от формы ! Ниже вы найдете формулы для всех шестнадцати форм, представленных в нашем калькуляторе площади. Для ясности мы перечислим только уравнения — их изображения, объяснения и выводы можно найти в отдельных абзацах ниже (а также в инструментах, посвященных каждой конкретной форме).
Вы готовы? Вот наиболее важные и полезные формулы площади для шестнадцати геометрических фигур:
- Квадрат Формула площади:
A = a² - Прямоугольник формула площади:
A = a * b - Формулы площади треугольника :
-
A = b * h / 2или -
A = 0,5 * a * b * sin (γ)или -
A = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))или -
A = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
-
- Формула площади круга :
A = πr² - Сектор круга Формула площади:
A = r² * угол / 2 - Эллипс Формула площади:
A = a * b * π - Трапеция Формула площади:
A = (a + b) * h / 2 - Формулы площади параллелограмма :
-
A = a * hили -
A = a * b * sin (угол)или -
A = e * f * sin (угол)
-
- Ромб Формулы площади:
-
A = a * hили -
A = (e * f) / 2или -
A = s² * sin (угол)
-
- Кайт формулы площади:
-
A = (e * f) / 2или -
A = a * b * sin (γ)
-
- Пентагон Формула площади:
A = a² * √ (25 + 10√5) / 4 - Шестиугольник Формула площади:
A = 3/2 * √3 * a² - Восьмиугольник Формула площади:
A = 2 * (1 + √2) * a² - Формула площади кольцевого пространства :
A = π (R² - r²) - Четырехугольник формула площади:
A = e * f * sin (угол) - Правильный многоугольник Формула площади:
A = n * a² * кроватка (π / n) / 4
Если ваша форма неправильная, попробуйте мысленно разделить ее на основные формы, для которых вы можете легко вычислить площадь.
Хотите изменить единицу площади? Просто нажмите на название устройства, и появится раскрывающийся список.
Формула площади
Вы забыли, что такое формула площади? Тогда вы попали в нужное место. Площадь квадрата равна длине его сторон:
-
Площадь квадрата = a * a = a², гдеa— сторона квадрата
Это самая основная и наиболее часто используемая формула, хотя существуют и другие.Например, есть формулы площади, в которых используются диагональ, периметр, радиус описанной окружности или внутренний радиус.
Формула площади прямоугольника
Формула площади прямоугольника тоже несложная задача — это просто умножение сторон прямоугольника:
Расчет площади прямоугольника чрезвычайно полезен в повседневных ситуациях: от строительства здания (оценка необходимой плитки, настила, сайдинга или определение площади крыши) до декорирования вашей квартиры (сколько краски или обоев мне нужно?) До расчета количества людей ваш листовой торт может накормить.
Формула площади треугольника
Существует множество различных формул для вычисления площади треугольника, в зависимости от того, что дано и какие законы или теоремы используются. В этом калькуляторе площади мы реализовали четыре из них:
1. Данные база и высота
-
Площадь треугольника = b * h / 2
2. Даны две стороны и угол между ними (SAS)
-
Площадь треугольника = 0,5 * a * b * sin (γ)
3.Учитывая три стороны (SSS) (Эта формула площади треугольника называется формулой Герона )
-
Площадь треугольника = 0,25 * √ ((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))
4. Даны два угла и сторона между ними (ASA)
-
Площадь треугольника = a² * sin (β) * sin (γ) / (2 * sin (β + γ))
Есть треугольник особого вида, прямоугольный.В этом случае основание и высота — это две стороны, которые образуют прямой угол. Тогда площадь прямоугольного треугольника может быть выражена как:
Площадь правого треугольника = a * b / 2
Формула площади круга
Формула площади круга — одна из самых известных формул:
-
Площадь круга = πr², гдеr— радиус окружности
В этом калькуляторе мы реализовали только это уравнение, но в нашем круговом калькуляторе вы можете рассчитать площадь по двум разным формулам:
- Диаметр
-
Площадь круга = πr² = π * (d / 2) ²
- Окружность
Кроме того, формула площади круга удобна в повседневной жизни — как серьезная дилемма, какой размер пиццы выбрать.
Формула площади сектора
Формулу площади сектора можно найти, взяв пропорцию круга. Площадь сектора пропорциональна его углу, поэтому, зная формулу площади круга, мы можем записать, что:
α / 360 ° = Площадь сектора / Площадь круга
Преобразование угла говорит нам, что 360 ° = 2π
α / 2π = Площадь сектора / πr²
так:
-
Площадь сектора = r² * α / 2
Формула площади эллипса
Чтобы найти формулу площади эллипса, сначала вспомните формулу площади круга: πr² .Для эллипса у вас есть не одно значение радиуса, а два разных значения: a и b . Единственная разница между формулой площади круга и эллипса заключается в замене r² произведением большой и малой полуосей, a * b :
-
Площадь эллипса = π * a * b
Формула площади трапеции
Площадь трапеции можно найти по следующей формуле:
-
Площадь трапеции = (a + b) * h / 2, гдеaиb— длины параллельных сторон, аh— высота
Также формула площади трапеции может быть выражена как:
Площадь трапеции = м * ч , где м — среднее арифметическое длин двух параллельных сторон
Площадь формулы параллелограмма
Если вы хотите рассчитать площадь с учетом основания и высоты, сторон и угла или диагоналей параллелограмма и угла между ними, вы находитесь в нужном месте.В нашем инструменте вы найдете три формулы площади параллелограмма:
1. Основание и высота
-
Площадь параллелограмма = a * h
2. Стороны и угол между ними
-
Площадь параллелограмма = a * b * sin (α)
3. Диагонали и угол между ними
-
Площадь параллелограмма = e * f * sin (θ)
Площадь формулы ромба
Мы реализовали три полезные формулы для вычисления площади ромба.Вы можете найти этот район, если знаете:
1. Сторона и высота
2. Диагонали
-
Площадь ромба = (e * f) / 2
3. Сторона и любой угол, например, α
-
Площадь ромба = a² * sin (α)
Площадь формулы воздушного змея
Для расчета площади воздушного змея можно использовать два уравнения, в зависимости от того, что известно:
- Площадь формулы воздушного змея по диагоналям змея
- Площадь формулы воздушного змея с учетом двух несовпадающих длин сторон и угла между этими двумя сторонами
-
Площадь змеевика = a * b * sin (α)
Формула площади пятиугольника
Площадь пятиугольника можно рассчитать по формуле:
-
Площадь пятиугольника = a² * √ (25 + 10√5) / 4, где a — сторона правильного пятиугольника
Ознакомьтесь с нашим специальным инструментом пятиугольник, в котором представлены другие важные свойства правильного пятиугольника: сторона, диагональ, высота и периметр, а также радиус описанной и вписанной окружности.
Площадь шестиугольника, формула
Основная формула площади шестиугольника:
-
Площадь шестигранника = 3/2 * √3 * a², где a — сторона правильного шестиугольника
Так откуда взялась формула? Вы можете представить себе правильный шестиугольник как набор из шести равносторонних равносторонних треугольников. Чтобы найти площадь шестиугольника, все, что нам нужно сделать, это найти площадь одного треугольника и умножить ее на шесть. Формула для площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленный на 4:
.
Площадь равностороннего треугольника = (a² * √3) / 4
Площадь шестиугольника = 6 * Площадь равностороннего треугольника = 6 * (a² * √3) / 4 = 3/2 * √3 * a²
Площадь восьмиугольника по формуле
Чтобы найти площадь восьмиугольника, все, что вам нужно сделать, это знать длину стороны и формулу ниже:
-
Площадь восьмиугольника = 2 * (1 + √2) * a²
Площадь восьмиугольника также можно рассчитать по:
Площадь восьмиугольника = периметр * апофема / 2
Периметр в восьмиугольном корпусе просто 8 * .А что такое апофема? Апофема — это расстояние от центра многоугольника до середины стороны. В то же время это высота треугольника, образованного линией от вершин восьмиугольника к его центру. Этот треугольник — один из восьми совпадающих — является равнобедренным треугольником, поэтому его высоту можно рассчитать, например, с помощью теоремы Пифагора по формуле:
h = (1 + √2) * a / 4
Итак, наконец, мы получаем первое уравнение:
Площадь восьмиугольника = периметр * апофема / 2 = (8 * a * (1 + √2) * a / 4) / 2 = 2 * (1 + √2) * a²
Площадь кольцевого пространства по формуле
Кольцо — это объект в форме кольца — это область, ограниченная двумя концентрическими окружностями разного радиуса.Найти формулу площади кольца — простая задача, если вы помните формулу площади круга. Вы только посмотрите: площадь кольца — это разница площадей большего круга радиуса R и меньшего радиуса r:
-
Площадь кольца = πR² - πr² = π (R² - r²)
Кстати, вы видели наш конвертер размеров колец?
Площадь четырехугольника
Четырехугольная формула, которую реализует этот калькулятор площади, использует две заданные диагонали и угол между ними.
-
Площадь четырехугольника = e * f * sin (α), где e, f — диагонали
Мы можем использовать любой из двух углов, так как мы вычисляем их синус. Зная, что два соседних угла являются дополнительными, мы можем утверждать, что sin (угол) = sin (180 ° - угол) .
Если вы ищете другие формулы для определения площади четырехугольника, воспользуйтесь нашим специальным инструментом для четырехугольника, где вы найдете формулу Бретшнайдера (с учетом четырех сторон и двух противоположных углов) и формулу, в которой используются бимедианы и угол между ними. .
Формула площади правильного многоугольника
Формула для площади правильного многоугольника выглядит следующим образом:
-
Площадь правильного многоугольника = n * a² * детская кроватка (π / n) / 4
где n — количество сторон, а — длина стороны.
Существуют и другие уравнения, в которых используются, например, такие параметры, как радиус описанной окружности или периметр. Вы можете найти эти формулы в специальном абзаце нашего калькулятора площади многоугольника.
Если вы имеете дело с неправильным многоугольником, помните, что вы всегда можете разделить фигуру на более простые фигуры.Просто посчитайте площадь каждого из них и в конце просуммируйте их. Разбиение многоугольника на набор треугольников называется триангуляцией многоугольника.
Площадь неправильных многоугольников
Введение
Я просто подумал, что поделюсь с вами умной техникой, которую когда-то использовал для определения площади общих многоугольников.
Многоугольник может быть правильным (все углы равны и все стороны равны) или неправильным
| Обычный | Нерегулярное |
Пример многоугольника
Давайте используем этот многоугольник в качестве примера:
Координаты
Первый шаг — превратить каждую вершину (угол) в координату, как на графике:
Площадь под однолинейным сегментом
Теперь для каждого сегмента линии проработайте область до оси x .
Итак, как рассчитать каждую площадь?
Усредните две высоты, затем умножьте на ширину
Пример. Для фигуры, выделенной выше, мы берем две высоты (координаты «y» 2,28 и 4,71) и вычисляем среднюю высоту:
(2,28 + 4,71) / 2 = 3,495
Определите ширину (разница между координатами «x» 2,66 и 0,72)
2,66-0,72 = 1,94
Площадь ширина × высота:
1.94 × 3,495 = 6,7803
Добавьте их всех
Теперь сложите их все!
Но фокус в том, чтобы складывать, когда они идут вперед (положительная ширина), и вычитать, когда они идут назад (отрицательная ширина).
Если вы всегда будете обходить многоугольник по часовой стрелке и всегда вычитаете первую координату «x» из второй, это работает естественным образом, например:
| из | по | |||||
|---|---|---|---|---|---|---|
| x | y | х | y | Средняя высота | Ширина (+/-) | Площадь (+/-) |
| 0.72 | 2,28 | 2,66 | 4,71 | 3,495 | 1,94 | 6,7803 |
| 2,66 | 4,71 | 5 | 3,5 | 4,105 | 2,34 | 9.6057 |
| 5 | 3,5 | 3,63 | 2,52 | 3,01 | -1.37 | -4,1237 |
| 3,63 | 2,52 | 4 | 1,6 | 2,06 | 0,37 | 0,7622 |
| 4 | 1,6 | 1,9 | 1 | 1,3 | -2,1 | -2,7300 |
| 1,9 | 1 | 0,72 | 2.28 | 1,64 | -1,18 | -1,9352 |
| Всего: | 8,3593 | |||||
Вы также можете пойти в другом направлении. Если у вас есть отрицательная область, просто сделайте ее положительной.
А это выглядит так:
Вот и все! Площадь .8 соток.3593
Инструмент «Площадь многоугольника»
Рад, что вы дочитали до этого места! Вы будете вознаграждены ссылкой на область инструмента рисования многоугольника, который может сделать все это за вас. Он также допускает ввод координат вручную.
Как рассчитать площадь участка или участка неправильной формы? / Расчет площади участка неправильной формы. (Часть-1) ~ ПАРАМЕТРЫ ВИДЕНИЯ
Теперь давайте рассмотрим некоторые из возможных неправильных форм земли или участка и давайте вычислим площадь этих участков, используя математические формулы.
Тип 1:
Здесь две стороны AD и BC параллельны друг другу, а все 4 стороны имеют разную длину.
Данные:
Боковой AD (a) = 16,105м.
Сторона BC (b) = 10м.
Сторона AB = 7м.
Боковой CD = 6,5 м.
Стороны AD и BC земли параллельны друг другу.
Расстояние по перпендикуляру между сторонами AD и BC (h) = 6 м.
Площадь земельного участка рассчитывается по формуле
= 1/2 × (a + b) × h
= 1/2 × (сторона AD + сторона BC) × Перпендикулярное расстояние
= 1/2 × (16.105 м + 10 м) × 6 м
= 1/2 × 26,105 м × 6 м
= 78,315 кв.
Примечание :
1. Формулу следует использовать только тогда, когда две стороны площадки параллельны друг другу.
2. Расстояние по перпендикуляру между двумя параллельными сторонами, т.е. h , можно измерить непосредственно на участке, если оно не известно.
Тип 2:
Здесь две стороны AD и BC параллельны друг другу, а сторона DC перпендикулярна этим двум параллельным сторонам.
Данные:
Боковой AD (a) = 13,6 м.
Сторона BC (b) = 10м.
Сторона AB = 7м.
Боковой CD (h) = 6м.
Стороны AD и BC земли параллельны друг другу.
Площадь земельного участка рассчитывается по формуле
= 1/2 × (a + b) × h
= 1/2 × (сторона AD + сторона BC) × сторона DC
= 1/2 × (13,6 м + 10 м) × 6 м
= 1/2 × 23,6 м × 6 м
= 70.8 кв.м.
Примечание:
1. Формулу следует использовать только тогда, когда две стороны площадки параллельны друг другу.
2. Нет необходимости измерять длину перпендикулярного расстояния, поскольку сторона DC соединяет две параллельные стороны под углом 90 °.
Альтернативный метод:
Давайте нарисуем перпендикулярную линию, соединяющую стороны AD и BC, как показано на рисунке выше.
Сторона BE = сторона DC = 6 м, поскольку обе перпендикулярны двум параллельным сторонам площадки.
Сторона AE = сторона AD — сторона BC
= 13,6 м — 10 м
= 3,6 м.
Теперь вычислим площадь треугольника AEB и площадь прямоугольника EDBC отдельно
Площадь треугольника AEB
= 1/2 × основание × высота
= 1/2 × сторона AE × сторона EB
= 1/2 × 3,6 м × 6 м
= 10,8 кв.
Площадь прямоугольника EDBC.
Здесь длина = сторона ED или сторона BC = 10 м
ширина = сторона EB или сторона DC = 6 м.
Площадь прямоугольника
= длина × ширина
= 10 м × 6 м
= 60 кв.
Итак, площадь земли
= площадь треугольника AFB + площадь прямоугольника EDBC
= 10,8 кв.м. + 60 кв.
= 70,8 кв.
(Ответ тот же, что и выше.)
Точно так же вы можете вычислить и подтвердить площадь типа 1 , построив два треугольника и один прямоугольник на первом рисунке.
.

 м. или 2 сотки.
м. или 2 сотки.
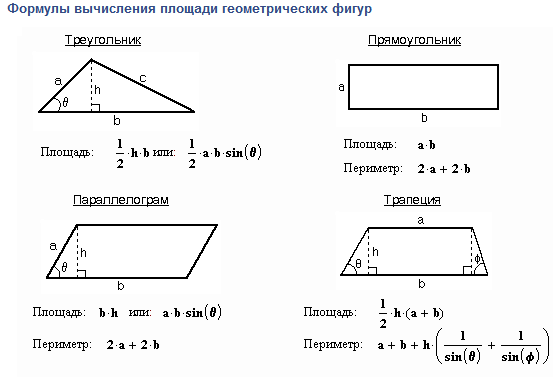 Это бесплатно.
Это бесплатно.
 Если компьютер под рукой, такой способ будет самым быстрым.
Если компьютер под рукой, такой способ будет самым быстрым.


 При этом может возникнуть проблема с определением длины криволинейного участка (например, части окружности). Конечно, можно воспользоваться специальными формулами для расчетов, но проще приложить плотно к стене гибкую рулетку и аккуратно зафиксировать ее показание. Все полученные величины необходимо сложить.
При этом может возникнуть проблема с определением длины криволинейного участка (например, части окружности). Конечно, можно воспользоваться специальными формулами для расчетов, но проще приложить плотно к стене гибкую рулетку и аккуратно зафиксировать ее показание. Все полученные величины необходимо сложить.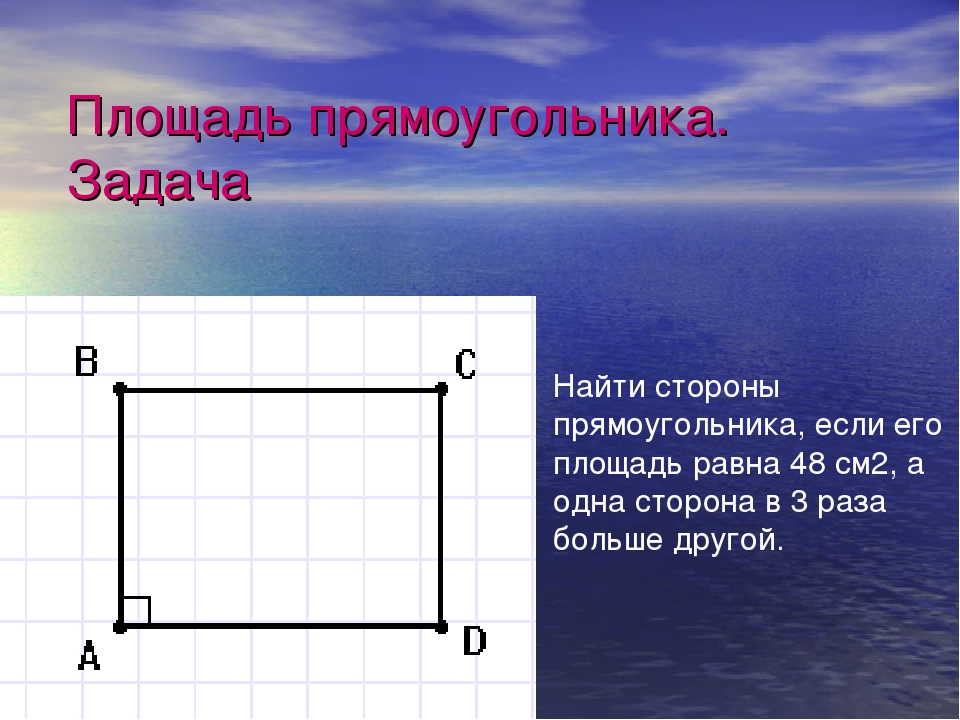

 Для этого нужно активировать данную субопцию, после чего здесь же обратиться к параметру «объекты» и в графическом поле выбрать замкнутые фигуры в нужном количестве.
Для этого нужно активировать данную субопцию, после чего здесь же обратиться к параметру «объекты» и в графическом поле выбрать замкнутые фигуры в нужном количестве.

 На бумаге диагональ от верхнего правого угла до нижнего левого угла составляет примерно 20 ярдов. От верхнего левого угла до нижнего правого угла примерно 22 ярда. На другом газоне ширина его вершины составляет 10 ярдов. Нижняя сторона 5 ярдов в поперечнике. Левая сторона составляет 30 ярдов, а правая - 32 ярда. Диагональ от верхнего правого угла до нижнего левого угла составляет примерно 31 ярд. От верхнего левого угла до нижнего правого примерно 33 ярда.
На бумаге диагональ от верхнего правого угла до нижнего левого угла составляет примерно 20 ярдов. От верхнего левого угла до нижнего правого угла примерно 22 ярда. На другом газоне ширина его вершины составляет 10 ярдов. Нижняя сторона 5 ярдов в поперечнике. Левая сторона составляет 30 ярдов, а правая - 32 ярда. Диагональ от верхнего правого угла до нижнего левого угла составляет примерно 31 ярд. От верхнего левого угла до нижнего правого примерно 33 ярда.  Высота лужайки составляет 14 ярдов (назовите это значение «а»).
Левая сторона составляет 16 ярдов (назовите это значение «b»).
Третья сторона треугольника - диагональ.
Диагональ от верхнего правого угла до нижнего левого угла
Высота лужайки составляет 14 ярдов (назовите это значение «а»).
Левая сторона составляет 16 ярдов (назовите это значение «b»).
Третья сторона треугольника - диагональ.
Диагональ от верхнего правого угла до нижнего левого угла  Если мы подключим a, b, c и s, мы получим:
sqrt [s (s-a) (s-b) (s-c)]
sqrt [24,5 (24,5-7) (24,5-22) (24,5-20)]
sqrt [24,5 (17,5) (2,5) (4,5)]
sqrt [4823.4375]
Площадь нижнего правого треугольника: 69,45 кв. ярда
Это означает, что общая площадь лужайки равна сумме двух треугольных площадей, в общей сложности 180,69 квадратных ярдов. Если 1 квадрат дерна равен 1 квадратному ярду, то вам понадобится 181 квадрат дерна (потому что вы не можете купить 0.69 квадратов дерна).
Если мы подключим a, b, c и s, мы получим:
sqrt [s (s-a) (s-b) (s-c)]
sqrt [24,5 (24,5-7) (24,5-22) (24,5-20)]
sqrt [24,5 (17,5) (2,5) (4,5)]
sqrt [4823.4375]
Площадь нижнего правого треугольника: 69,45 кв. ярда
Это означает, что общая площадь лужайки равна сумме двух треугольных площадей, в общей сложности 180,69 квадратных ярдов. Если 1 квадрат дерна равен 1 квадратному ярду, то вам понадобится 181 квадрат дерна (потому что вы не можете купить 0.69 квадратов дерна).  И вообще, площадь чего угодно можно вычислить, если разбить ее на треугольники.
И вообще, площадь чего угодно можно вычислить, если разбить ее на треугольники. 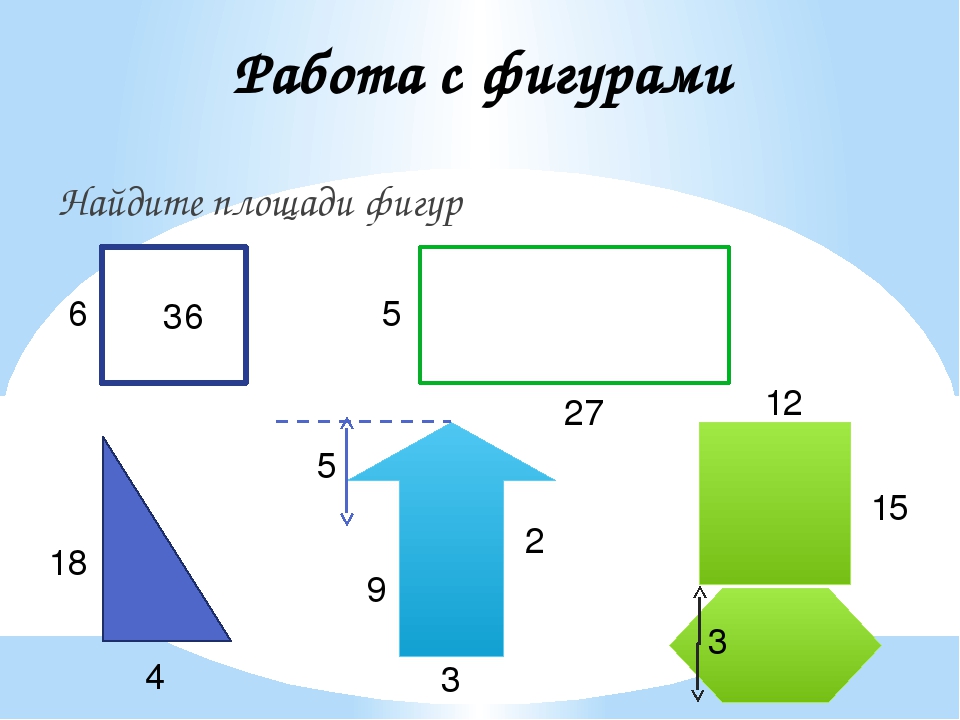 195215 ...),
= 62,651378 ... квадратных футов.
Тогда сумма будет
А = А1 + А2 = 5016.350378 ... квадратных футов,
что равняется максимально возможному значению 5016.35054787 ... до трех десятичных знаков (но не точно).
Не стесняйтесь писать еще раз, если я могу еще помочь.
195215 ...),
= 62,651378 ... квадратных футов.
Тогда сумма будет
А = А1 + А2 = 5016.350378 ... квадратных футов,
что равняется максимально возможному значению 5016.35054787 ... до трех десятичных знаков (но не точно).
Не стесняйтесь писать еще раз, если я могу еще помочь. 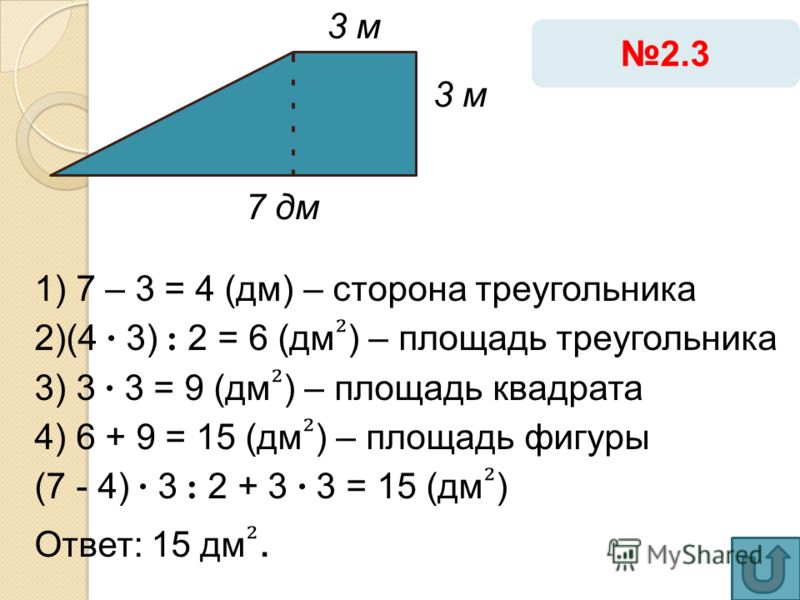 Проложите и измерьте линию любой длины
Проложите и измерьте линию любой длины  Вы, конечно же, хотите знать КАК?
Я не знаком ни с одним традиционным методом, используемым геодезистами, но я, по крайней мере, могу придумать метод, который будет работать.Требуется два шага.
Во-первых, если мы выберем систему координат, в которой один конец базовой линии является началом, а другой - точкой (d, 0), мы можем найти координаты каждой вершины. Я использовал эту цифру:
п
+
/ | \
/ | \
/ | \
/ | у \
/ | \
/ | \
/ а | б \
+ ------- + --------------- +
А х г-х Б
написать два уравнения
у / х = загар (а)
у / (д-х) = загар (б)
из которых я получил формулы
д д
x = ---------- и y = ---------------
загар (а) 1 1
------ + 1 ------ + ------
загар (б) загар (а) загар (б)
Вы можете проверить их; Я сделал это довольно быстро, но это дает представление.Случаи, когда касательные равны нулю или бесконечны, обрабатываются легко.
Вы, конечно же, хотите знать КАК?
Я не знаком ни с одним традиционным методом, используемым геодезистами, но я, по крайней мере, могу придумать метод, который будет работать.Требуется два шага.
Во-первых, если мы выберем систему координат, в которой один конец базовой линии является началом, а другой - точкой (d, 0), мы можем найти координаты каждой вершины. Я использовал эту цифру:
п
+
/ | \
/ | \
/ | \
/ | у \
/ | \
/ | \
/ а | б \
+ ------- + --------------- +
А х г-х Б
написать два уравнения
у / х = загар (а)
у / (д-х) = загар (б)
из которых я получил формулы
д д
x = ---------- и y = ---------------
загар (а) 1 1
------ + 1 ------ + ------
загар (б) загар (а) загар (б)
Вы можете проверить их; Я сделал это довольно быстро, но это дает представление.Случаи, когда касательные равны нулю или бесконечны, обрабатываются легко.  Для этого есть стандартная формула:
A = [(x1y2 + x2y3 + ... + xny1) - (y1x2 + y2x3 + ... + ynx1)] / 2
Я думаю, этого должно быть достаточно - может быть, не так элегантно, как могло бы быть, но довольно просто.
Для этого есть стандартная формула:
A = [(x1y2 + x2y3 + ... + xny1) - (y1x2 + y2x3 + ... + ynx1)] / 2
Я думаю, этого должно быть достаточно - может быть, не так элегантно, как могло бы быть, но довольно просто. 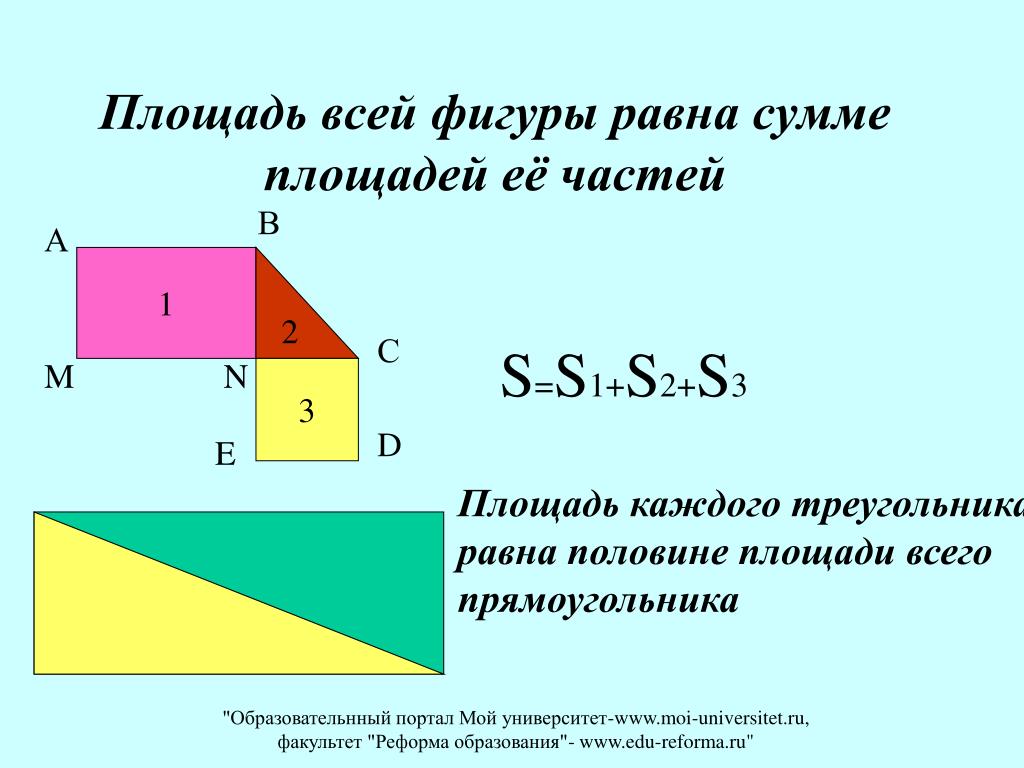 Юридическое описание составляет 15,8 акров.
Как я могу определить площадь в квадратных футах?
Юридическое описание составляет 15,8 акров.
Как я могу определить площадь в квадратных футах? 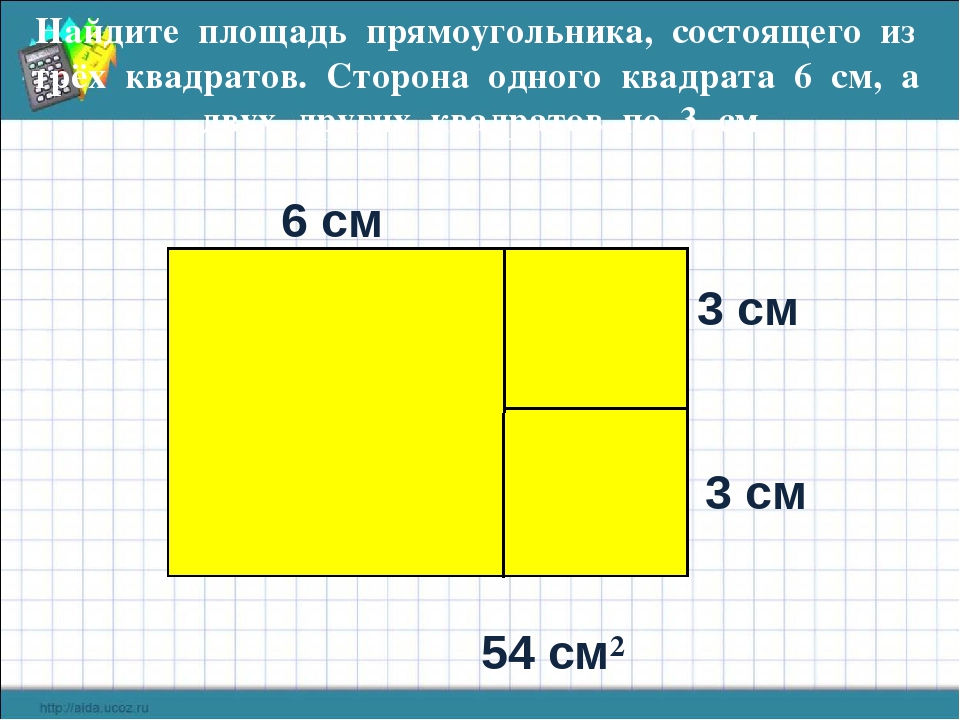 04 фут - с.ш.38 град. 15 '00 "в.д.
1950,16 ft - на платформе написано: S 80 deg 36 '34 "E.
338,47 футов - на платформе указано: S 30 градусов 59 '49 дюймов з.д.
200.75 пт - N 80 град 42 '11 "з.д.
Надеюсь это поможет; это все, что есть на планшете.
04 фут - с.ш.38 град. 15 '00 "в.д.
1950,16 ft - на платформе написано: S 80 deg 36 '34 "E.
338,47 футов - на платформе указано: S 30 градусов 59 '49 дюймов з.д.
200.75 пт - N 80 град 42 '11 "з.д.
Надеюсь это поможет; это все, что есть на планшете.  ш. 80 град. 36 '34 "в.д. -> 180–80,61 = 99,391 град.
CD: ю. Ш. 30 град. 59 '49 "з. Д. -> 180 + 30,997 = 210,997 град.
DA: с.ш. 80 град. 42 '11 "з.д. -> 360–80,703 = 279,297 град.
Это должно выглядеть примерно так
B ----_____ 1950
363 / -----_____
/ ---- С
A ----_____ /
-----_____ / 338
2000 ---- D
ш. 80 град. 36 '34 "в.д. -> 180–80,61 = 99,391 град.
CD: ю. Ш. 30 град. 59 '49 "з. Д. -> 180 + 30,997 = 210,997 град.
DA: с.ш. 80 град. 42 '11 "з.д. -> 360–80,703 = 279,297 град.
Это должно выглядеть примерно так
B ----_____ 1950
363 / -----_____
/ ---- С
A ----_____ /
-----_____ / 338
2000 ---- D  . + x1yn)] / 2
Это делает область
К = [(0 * 224.2 на акр, дает 14,34 акра.
Неудивительно, что геодезист, похоже, правильно использовал свои собственные данные.
. + x1yn)] / 2
Это делает область
К = [(0 * 224.2 на акр, дает 14,34 акра.
Неудивительно, что геодезист, похоже, правильно использовал свои собственные данные.