Содержание
Площадь четырехугольника
Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.
В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.
Таблица с формулами площади четырехугольника (в конце страницы)
— Вычисления (показано)
(скрыто)
— примечания (показано)
(скрыто)
1
Площадь четырехугольника по диагоналям и углу между ними
… подготовка …
d1 — диагональ
d2 — диагональ
α° — угол между диагоналями
2
Площадь четырехугольника через стороны и углы между этими сторонами
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
. .. подготовка …
.. подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
3
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты
Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
4
Площадь четырехугольника в который можно вписать окружность
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
r — радиус вписанной окружности
5
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними
Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.
… подготовка …
a — сторона
b — сторона
c — сторона
d — сторона
α° — угол между сторонами
β° — угол между сторонами
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин».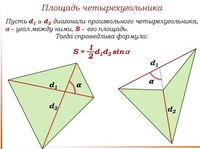 Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади четырехугольника
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
Определения
Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т. д.
д.
Площадь прямоугольника в чем измеряется. Как найти площадь прямоугольника. Площадь неправильного четырехугольника с заданными сторонами
Площадь многоугольника
Понятие площади многоугольника будем связывать с такой геометрической фигурой, как квадрат. За единицу площади многоугольника будем принимать площадь квадрата со стороной, равной единице. Введем два основных свойства, для понятия площади многоугольника.
Свойство 1:
Для равных многоугольников значения их площадей равны.
Свойство 2:
Любой многоугольник можно разбить на несколько многоугольников. При этом площадь исходного многоугольника равняется сумме площадей всех многоугольников, на которые разбит данный многоугольник.
Площадь квадрата
Теорема 1
Площадь квадрата определяется как квадрат длины его стороны.
где $a$ — длина стороны квадрата.
Доказательство.
Для доказательства нам необходимо рассмотреть три случая.
Теорема доказана.
Площадь прямоугольника
Теорема 2
Площадь прямоугольника определяется произведением длин его смежных сторон.
Математически это можно записать следующим образом
Доказательство.
Пусть нам дан прямоугольник $ABCD$, у которого $AB=b,\ AD=a$. Достроим его до квадрата $APRV$, длина стороны которого равняется $a+b$ (рис. 3).
Рисунок 3.
По второму свойству площадей имеем
\ \ \
По теореме 1
\ \
Теорема доказана.
Пример задач
Пример 1
Найти площадь прямоугольника со сторонами $5$ и $3$.
Для вычисления площади и периметра квадрата нужно разобраться в понятиях этих величин. Квадрат представляет собой прямоугольник только с четырьмя одинаковыми сторонам, которые имеют между собой угол в 90°. Периметр — это сумма длин всех сторон. Площадь — это произведение длины прямоугольной фигуры на ее ширину.
Площадь квадрата и как ее найти
Как было сказано выше, квадрат — это прямоугольник, имеющий 4 равные стороны, поэтому ответом на вопрос: «как найти площадь квадрата» является формула: S = a*a или S = a
2
, где а — сторона квадрата. Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Исходя из этой формулы, легко находится сторона квадрата, если известна площадь. Для этого необходимо извлечь квадрат из указанной величины.
Например, S = 121, следовательно, а = √121 = 11. Если заданное значение отсутствует в таблице квадратов, то можно воспользоваться калькулятором: S = 94, а = √94 = 9,7.
Как найти периметр квадрата
Периметр квадрата находится по легкой формуле: Р = 4а, где а — сторона квадрата.
Пример:
- сторона квадрата = 5, следовательно, P = 4*5 = 20
- сторона квадрата = 3, следовательно, Р = 4*3 = 12
Но существуют такие задачи, где заведомо обозначена площадь, а нужно найти периметр. При решении нужны формулы, которые представлены ранее.
Например: как найти периметр квадрата, если известна площадь, равная 144?
Шаги решения:
- Выясняем длину одной стороны: а = √144 = 12
- Находим периметр: Р = 4*12 = 48.
Нахождение периметра вписанного квадрата
Существуют еще несколько способов нахождения периметра квадрата. Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Рассмотрим один из них: нахождение периметра через радиус описанной окружности. Здесь появляется новый термин «вписанный квадрат» — это квадрат, чьи вершины лежат на окружности.
Алгоритм решения:
- так как на рассмотрении квадрат, формулу можно выразить таким образом: a
2
+ a
2
= (2r)
2
; - затем следует уравнение сделать проще: 2a
2
= 4(r)
2
; - делим уравнение на 2: (a
2
) = 2(r)
2
; - извлекаем корень: a = √(2r).
В итоге получаем последнюю формулу: а (сторона квадрата) = √(2r).
- Найденная сторона квадрата умножается на 4, далее применяется стандартная формула по нахождению периметра: P = 4√(2r).
Задача:
Дан квадрат, который вписан в окружность, ее радиус равен 5. Значит, диагональ квадрата равняется 10. Применяем теорему Пифагора: 2(a
2
) = 10
2
, то есть 2a
2
= 100. Делим полученное на два и в результате: a
2
= 50. Так как это не табличное значение, используем калькулятор: а = √50 = 7,07. Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Умножаем на 4: Р = 4*7,07 = 28,2. Задача решена!
Рассмотрим еще один вопрос
Часто в задачах встречается другое условие: как найти площадь квадрата, если известен периметр?
Мы уже рассмотрели все необходимые формулы, поэтому для решения задач подобного типа, необходимо умело их применять и связывать между собой. Перейдем сразу к наглядному примеру: Площадь квадрата равна 25 см
2
, найдите его периметр.
Шаги решения:
- Находим сторону квадрата: а = √25 = 5.
- Находим сам периметр: Р = 4*а = 4*5 = 20.
Подводя итог, важно напомнить, что такие легкие формулы применимы не только в учебной деятельности, но и повседневной жизни. Периметр и площадь фигуры дети учатся находить еще в начальной школе. В средних классах появляется новый предмет — геометрия, где теорема Пифагора находится в самом начале изучения. Эти азы математики проверяются и по окончанию школы ОГЭ и ЕГЭ, поэтому важно знать эти формулы и правильно их применять.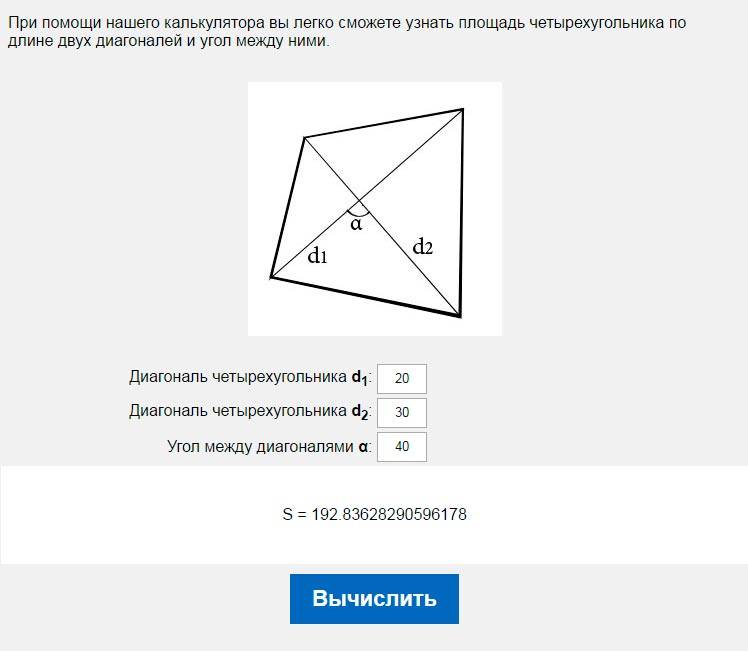
С таким понятием, как площадь, нам приходится сталкиваться в своей жизни повседневно. Так, например, при строительстве дома ее нужно знать для того, чтобы рассчитать количество необходимого материала. Размер садового участка также будет характеризоваться площадью. Даже ремонт в квартире невозможно сделать без этого определения. Поэтому вопрос, как найти площадь прямоугольника, на нашем встает очень часто и является важным не только для школьников.
Для тех, кто не знает, прямоугольник — это плоская фигура, у которой противоположные стороны равны, а углы составляют 90о. Для обозначения площади в математике используют английскую букву S. Ее измеряют в квадратных единицах: метрах, сантиметрах и так далее.
Теперь попытаемся дать подробный ответ на вопрос, как найти площадь прямоугольника. Существует несколько способов определения этой величины. Наиболее часто мы сталкиваемся со способом определения площади с помощью ширины и длины.
Возьмем прямоугольник с шириной b и длиной k. Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
Для вычисления площади данного прямоугольника необходимо ширину умножить на длину. Это все можно представить в виде формулы, которая будет выглядеть так: S = b * k.
А теперь рассмотрим этот способ на конкретном примере. Необходимо определить площадь садового участка с шириной 2 метра и длиной 7 метров.
S = 2 * 7 = 14 м2
В математике, особенно в приходится определять площадь иными способами, так как во многих случаях ни длина, ни ширина прямоугольника нам не известна. Вместе с тем имеют место другие известные величины. Как найти площадь прямоугольника в этом случае?
- Если нам известна длина диагонали и один из углов, составляющий диагональ с любой стороной прямоугольника, то в этом случае потребуется вспомнить о площади Ведь если разобраться, то прямоугольник состоит из двух равных прямоугольных треугольников. Итак, вернемся к определяемой величине. Для начала необходимо определить косинус угла. Полученную величину умножить на длину диагонали. В итоге получим длину одной из сторон прямоугольника.
 Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
В виде формулы это будет выглядеть так:
S = cos(a) * sin(a) * d2 , где d- длина диагонали
- Еще один способ определения площади прямоугольника — через вписанную в него окружность. Он применяется в том случае, если прямоугольник является квадратом. Для использования данного способа необходимо знать Как вычислить площадь прямоугольника таким способом? Конечно же, по формуле. Доказывать мы ее не будем. А выглядит она так: S = 4 * r2, где r -радиус.
Случается так, что вместо радиуса нам известен диаметр вписанной окружности. Тогда формула будет выглядеть так:
S=d2,где d — диаметр.
- Если известна одна из сторон и периметр, то как узнать площадь прямоугольника в этом случае? Для этого необходимо произвести ряд простых вычислений. Как мы знаем, противоположные стороны прямоугольника равны, поэтому от значения периметра необходимо отнять известную длину, умноженную на два.
 Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
S=b* (P — 2*b), где b — длина стороны, P — периметр.
Как видим площадь прямоугольника можно определять различными способами. Все зависит от того, какие величины нам известны перед рассмотрением данного вопроса. Конечно же, последние методы исчисления в жизни практически не встречаются, но могут пригодиться для решений многих задач в школе. Возможно, и для решения ваших задач эта статья окажется полезной.
Урок на тему: «Формулы определения площади треугольника, прямоугольника, квадрата»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 5 класса
Тренажер к учебнику И. И.Зубаревой и А.Г.Мордковича
И.Зубаревой и А.Г.Мордковича
Тренажер к учебнику Г.В.Дорофеева и Л.Г.Петерсона
Определение и понятие площади фигуры
Чтобы лучше понять, что такое площадь фигуры, рассмотрим рисунок.
Эта произвольная фигура разбита на 12 маленьких квадратика. Сторона каждого квадратика равна 1 см. А площадь каждого квадратика равна 1 квадратному сантиметру, что записывается так:
1 см 2 .
Тогда площадь фигуры равна 12 квадратным сантиметрам. В математике площадь обозначается латинской буквой S.
Значит, площадь нашей фигуры равна: S фигуры = 12 см 2 .
Площадь фигуры равна площади всех маленьких квадратиков, из которых она состоит!
Ребята, запомните!
Площадь измеряется квадратными единицами длины.
Единицы измерения площади:
1. Квадратный километр — км 2 (когда площади очень большие, например, страна или море).
2. Квадратный метр — м 2 (вполне подходит для того, чтобы измерять площадь участка или квартиры).
3. Квадратный сантиметр — см 2 (обычно используется на уроках математики, когда рисуют фигуры в тетради).
4. Квадратный миллиметр — мм 2 .
Площадь треугольника
Рассмотрим два вида треугольников: прямоугольный и произвольный.
Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.
В нашем примере стороны равны 7 см и 4 см.
Формула для расчета площади треугольника записывается так:
S прямоугольного треугольника АВС = ВС * СА: 2
S прямоугольного треугольника АВС = 7 см * 4 см: 2 = 14 см 2
Теперь рассмотрим произвольный треугольник.
Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S произвольного треугольника АВС = ВС * h: 2.
Подставим в формулу наши данные и получим:
S произвольного треугольника АВС = 8 см * 6 см: 2 = 24 см 2 .
Площадь прямоугольника и квадрата
Возьмем прямоугольник АВСD со сторонами 5 см и 8 см.
Формула расчета площади прямоугольника записывается так:
S прямоугольника АВСD = АВ * ВС.
S прямоугольника АВСD = 8 см * 5 см = 40 см 2 .
Теперь рассчитаем площадь квадрата. В отличии от прямоугольника и треугольника, для нахождения площади квадрата необходимо знать только одну сторону. В нашем примере сторона квадрата ABCD равна 9 см.
S квадрата АВСD = АВ * ВС = АВ 2 .
Подставим в формулу наши данные и получим:
S квадрата АВСD = 9 см * 9 см = 81 см 2 .
Рассчитать площадь прямоугольника с подробным решением. Калькулятор находит площадь по формуле через длину и ширину прямоугольника. Основные способы и объяснение формул, по которым вы сможете самостоятельно решить свои задачи.
Онлайн-калькулятор
Вначале давайте разберемся с определением. У прямоугольника есть 4 стороны. Каждая сторона равна противоположной и параллельна ей. Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.
Здесь важно понимать, что все 4 стороны не могут быть равны, иначе получится квадрат. В прямоугольнике будут 2 одинаковые стороны одной длины и 2 одинаковые другой.
Все 4 угла, находящиеся внутри прямоугольника, — прямые. То есть каждый угол равен 90°.
Формула площади прямоугольника через его стороны
Чтобы найти площадь S S
S
прямоугольника, нужно перемножить две его стороны: сторону a a
a
умножаем на сторону b b
b
.
S = a ⋅ b . S = a \cdot b.
S
=
a
⋅
b
.
Пример
У нас есть прямоугольник A B C D ABCD
A
B
C
D
. Одна его сторона A B AB
A
B
равна 5 5
5
см, вторая B C BC
B
C
равна 3 3
3
см. Нам нужно найти его площадь S S
S
.
Решение:
Чтобы найти площадь S S
S
, нужно умножить сторону A B AB
A
B
на сторону B C BC
B
C
и получаем: S = 5 ⋅ 3 S = 5 \cdot 3
S
=
5
⋅
3
.
Ответ
: S = 15 S = 15
S
=
1
5
см 2 .
Формула площади прямоугольника через диагонали
S = 1 2 d 2 sin α . {\circ} = \frac{1}{2} \cdot 64 \cdot \frac{1}{2} = \frac{64}{4} = 16
{\circ} = \frac{1}{2} \cdot 64 \cdot \frac{1}{2} = \frac{64}{4} = 16
S
=
2
1
⋅
8
2
⋅
sin
3
0
∘
=
2
1
⋅
6
4
⋅
2
1
=
4
6
4
=
1
6
Ответ: S = 16 S = 16
S
=
1
6
см 2 .
Калькулятор расчета площади треугольного помещения
При расчете площадей помещений или других поверхностей, подлежащих отделке, порой приходится сталкиваться с многоугольными фигурами, которые неопытного человека могут поставить в тупик. Но на самом деле – нет ничего сложного, существует простой и точный способ провести необходимые вычисления.
Калькулятор расчета площади треугольного помещения
Любой многоугольник можно одной или несколькими линиями разбить на определенное количество треугольников, затем просчитать площади этих участков и просуммировать. А чтобы вычисления были произведены быстро и точно, примените предлагаемый калькулятор расчета площади треугольного помещения.
Несколько пояснений по работе с ним будут даны ниже.
Калькулятор расчета площади треугольного помещения
Перейти к расчётам
Несколько необходимых пояснений
Треугольные помещения встречаются нечасто, но калькулятор может быть полезен и в иных случаях. Как уже говорилось, на треугольники несложно разбить любую многоугольную плоскую фигуру.
Как уже говорилось, на треугольники несложно разбить любую многоугольную плоскую фигуру.
Пример разбивки неправильного четырёхугольника на два треугольника
Площадь треугольника чаще определяют произведением основания на высоты с последующим делением на два. Однако, в условиях стройки или ремонта пробить перпендикуляр, чтобы точно измерить высоту фигуры – не всегда бывает просто, если нет специальных инструментов. Даже небольшая ошибка в разметке способна привести к искажению конечного результата. Поэтому в данном случае применена формула Герона, позволяющая рассчитать площадь абсолютно любого треугольника по длинам трех его сторон, измерить которые – уже труда никакого не составит.
Значения запрашиваются в сантиметрах. Конечный результат – в квадратных метрах.
Если необходимо определит площадь прямоугольного или трапециевидного помещения, то есть у которого хотя бы одна пара сторон – параллельны друг другу, то для этого проще применить специальный калькулятор для четырехугольника. Он, кстати, учитывает возможное наличие выступов, колонн, ниш и других элементов, увеличивающих или уменьшающих общую площадь комнаты.
Он, кстати, учитывает возможное наличие выступов, колонн, ниш и других элементов, увеличивающих или уменьшающих общую площадь комнаты.
Существуют и более сложные случаи расчета площадей
Иногда приходится прибегать и к более сложным расчетам, когда некоторым стенам или элементам конструкции придана криволинейная форма. Как вычислить площадь комнаты при таких условиях – рассказывается в специальной публикации нашего портала.
Как измерить площадь — Наука
Наука 2021
Вы можете найти площадь любой двумерной фигуры, используя простые алгебраические формулы. Фактическая формула будет отличаться в зависимости от типа фигуры. Как только вы узнаете, как найти область ос
Содержание:
Вы можете найти площадь любой двумерной фигуры, используя простые алгебраические формулы. Фактическая формула будет отличаться в зависимости от типа фигуры. Как только вы узнаете, как найти область основных фигур, вы можете применить эти формулы, когда вам нужно найти область более сложных многоугольников. 2. Следовательно, общая площадь будет 25.
2. Следовательно, общая площадь будет 25.
Площадь прямоугольника
Вы можете найти площадь прямоугольника с формулой, длиной x шириной или l x w.Например, уравнение для прямоугольника с длиной 6 и шириной 8 будет 6×8. Следовательно, площадь будет 48.
Площадь неправильного многоугольника
Для неправильных многоугольников, таких как два смежных прямоугольника или L-образный многоугольник, вы можете найти область каждой фигуры отдельно, а затем добавить их. Например, площадь L-образного многоугольника, в которой площадь одного прямоугольника равна 5×3, а другого — 9×2, будет равна 5×3 + 9×2 или 15 + 18 = 33. Следовательно, общая площадь многоугольника будет быть 33.
Площадь треугольника
Вы можете найти площадь треугольника, используя формулу base x height / 2. Например, площадь треугольника с основанием 10 и высотой 7 будет 10×7 / 2. Поэтому общая площадь будет 35 ,
Площадь круга
Вы можете найти площадь круга, используя формулу pi x radius ^ 2 или pi x r ^ 2. 2. Следовательно, общая площадь будет приблизительно 28,28.
2. Следовательно, общая площадь будет приблизительно 28,28.
Формула Пика
Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.
Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.
В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.
Площадь искомой фигуры можно найти по формуле:
М – количество узлов на границе треугольника (на сторонах и вершинах)
N – количество узлов внутри треугольника
*Под «узлами» имеется ввиду пересечение линий.
Найдём площадь треугольника:
Отметим узлы:
1 клетка = 1 см
M = 15 (обозначены красным)
N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма:
Найдём площадь параллелограмма:
Отметим узлы:
M = 18 (обозначены красным)
N = 20 (обозначены синим)
Найдём площадь трапеции:
Отметим узлы:
M = 24 (обозначены красным)
N = 25 (обозначены синим)
Найдём площадь многоугольника:
Отметим узлы:
M = 14 (обозначены красным)
N = 43 (обозначены синим)
Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.
А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.
Теперь взгляните на следующие фигуры:
Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:
Отметим узлы:
M = 11 (обозначены красным)
N = 5 (обозначены синим)
Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.
Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.
Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ».
Найдём площадь фигуры:
Опишем около неё прямоугольник:
Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5
В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё.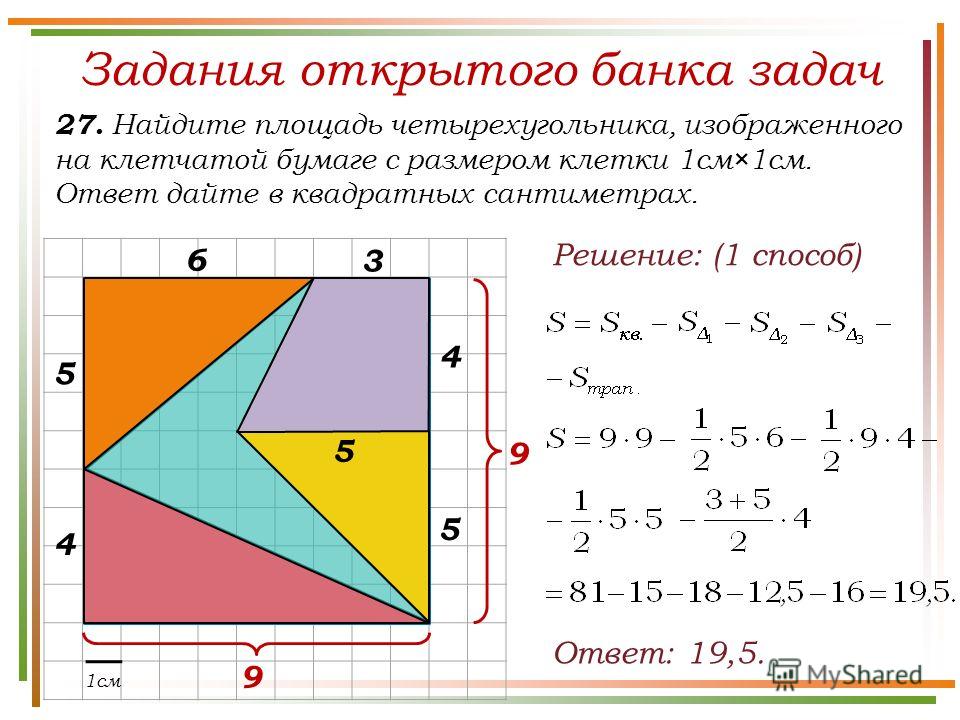 Успехов вам!
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как рассчитать площадь неправильного земельного участка
Для измерения участка непрямоугольной формы его делят на несколько разных фигур (как правило, это трапеции и квадраты). Затем по отдельности находят площадь каждой фигуры, складывают их и полученную сумму делят на 100 (такое деление выражает готовый результат в сотках). Полученное в итоге значение является площадью земельного участка.
Произвести такие расчеты самостоятельно бывает сложно, поэтому чаще всего для геодезических работ привлекают специалистов. В их арсенале имеются измерительные приборы, прошедшие специальную сертификацию:
- дальномеры;
- тахеометры;
- вышки для измерения высоты;
- нивелиры;
- лазерные рулетки.
По договоренности специалисты занимаются документальным оформлением полученных результатов. Для этого используются механический и аналитический методы расчетов. Аналитический метод является более точным, поскольку учитывает любые геометрические неровности участка (изломы, углы и т. д.). Однако на практике часто используют механический метод, так как он позволяет гораздо быстрее вычислить площадь участка.
Для этого используются механический и аналитический методы расчетов. Аналитический метод является более точным, поскольку учитывает любые геометрические неровности участка (изломы, углы и т. д.). Однако на практике часто используют механический метод, так как он позволяет гораздо быстрее вычислить площадь участка.
Задача профессиональных геодезистов — грамотно объединить эти два метода для повышения эффективности работ. Специалисты ООО «Кадастровое бюро» объединяют в своей практике аналитический и механический подходы в сочетании с современным оборудованием. Жители Москвы и Краснодара могут заказать измерение площади участка любой формы с составлением его детального плана. Наши инженеры имеют достаточный опыт и все необходимые допуски. Мы производим топографические работы для любых целей и в любых масштабах.
От чего зависят масштабы топографических работ?
Масштабы работ определяются целью измерений. Например, при формировании карт крупных промышленных предприятий или населенных пунктов используется масштаб 1:2000. Если измерению подлежит территория, прилегающая к инженерным коммуникациям, применятся масштаб 1:500. Самым детальным считается масштаб 1:200. Это крупная съемка, и она учитывает любые здания, постройки и прочие элементы земельного участка.
Если измерению подлежит территория, прилегающая к инженерным коммуникациям, применятся масштаб 1:500. Самым детальным считается масштаб 1:200. Это крупная съемка, и она учитывает любые здания, постройки и прочие элементы земельного участка.
Как мы работаем?
Сотрудничество с заказчиком начинается с оформления технического задания инженерам и подписания договора с компанией. Затем сотрудники ООО «Кадастровое бюро» согласовывают будущую съемку в местном органе архитектуры и составляют план действий.
Топографические работы включают внешний осмотр местности и подбор опорных геодезических точек для обоснования съемки, непосредственно съемку и контроль полученных результатов.
По завершении работ клиент получает отчет с приложением плана местности и модели земельного участка в электронном виде.
Узнать больше
Стоимость топографических работ опубликована в прайс-листе на сайте компании.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | a и b – смежные стороны | |
Посмотреть вывод формулы | d – диагональ, | ||
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | ||
| Параллелограмм | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | d – диагональ квадрата | ||
S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = a2 sin φ Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
S = 2ar Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | r – радиус вписанной окружности, | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания, | |
| S = m h | m – средняя линия, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
Посмотреть вывод формулы | a и b – основания, | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны, | |
a и b – неравные стороны, | |||
S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | , Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
S = ab где | |
где Посмотреть вывод формулы | |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R | |
| Параллелограмм | |
S = a ha где Посмотреть вывод формулы | |
S = absin φ где Посмотреть вывод формулы | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Квадрат | |
| S = a2 где | |
| S = 4r2 где | |
где Посмотреть вывод формулы | |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R | |
| Ромб | |
S = a ha где Посмотреть вывод формулы | |
S = a2 sin φ где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2ar где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Трапеция | |
где Посмотреть вывод формулы | |
S = m h где | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Дельтоид | |
S = ab sin φ где | |
где | |
S = (a + b) r где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный выпуклый четырёхугольник | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Вписанный четырёхугольник | |
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты | |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности.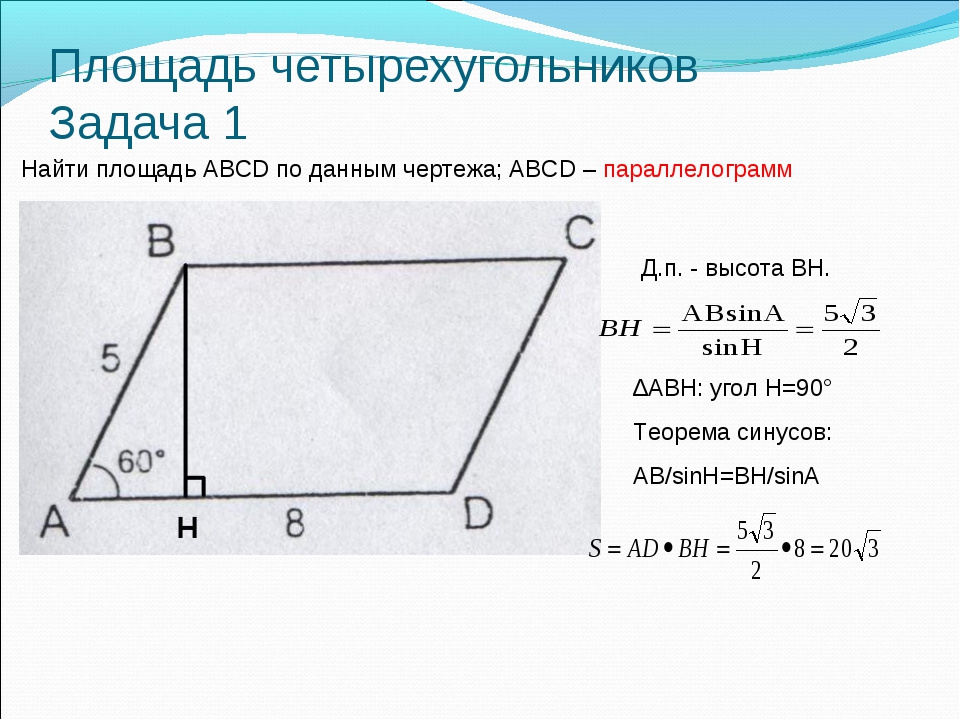 Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,
где a и b – основания, а c и d – боковые стороны трапеции,
(рис.6).
Рис. 6
6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,
что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как рассчитать площадь четырехугольника
Площадь четырехугольника описывает поверхность двумерной формы. Площадь можно представить как количество плиток, необходимое для покрытия пола, или количество краски, необходимое для стены. Чтобы найти площадь четырехугольника, тщательно измерьте длину, ширину и высоту фигуры и используйте соответствующую формулу для конкретного типа четырехугольника.
Площадь квадрата и прямоугольника
Чтобы вычислить площадь квадрата или прямоугольника, вам необходимо знать размеры сторон.Стороны квадрата равны, поэтому формула: с в квадрате = площади. S представляет собой длину одной стороны. Если сторона 4 дюйма, тогда площадь будет 4 x 4, что равно 16 дюймам в квадрате.
Чтобы найти площадь прямоугольника, умножьте длину горизонтальной стороны на длину вертикальной стороны. Используйте формулу ширина x высота = площадь . Если ширина 4 дюйма, а высота 2 дюйма, площадь равна 8 дюймам в квадрате.
Площадь ромба и параллелограмма
Хотя у ромба все стороны равны, а у параллелограмма две пары равных сторон, формула для площади одинакова.Формула: основание x высота = площадь. База представляет собой длину нижней стороны.
В отличие от формулы для квадрата или прямоугольника, высота не представляет собой длину вертикальной стороны. Проведите перпендикулярную линию от основания фигуры до верхней линии. Измерение этой вертикальной линии — это высота фигуры.
Если размер основания 4 дюйма, а высота 3 дюйма, то площадь фигуры составляет 12 дюймов в квадрате.
Площадь трапеции
Трапеция — это четырехугольник с двумя неравными параллельными сторонами.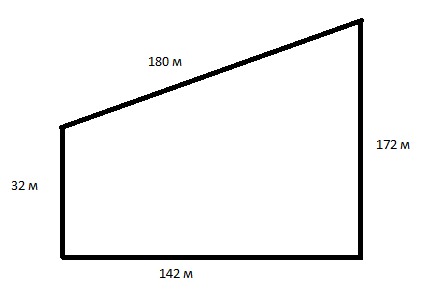 Формула такая же, если непараллельные стороны правильные или неправильные. Формула: ½ (a + b) x h. Буква a представляет длину верхней стороны, b представляет длину нижней стороны и h представляет высоту по вертикали.
Формула такая же, если непараллельные стороны правильные или неправильные. Формула: ½ (a + b) x h. Буква a представляет длину верхней стороны, b представляет длину нижней стороны и h представляет высоту по вертикали.
Высота фигуры — это не длина стороны, а длина вертикальной линии, перпендикулярной верхней и нижней сторонам.
Чтобы решить формулу, в которой длина a равна 3 дюймам, длина b равна 5 дюймам, а высота равна 4 дюймам, следуйте порядку операций и сначала сложите 3 + 5.Затем возьмите эту сумму, 8, и умножьте ее на ½, чтобы получить 4.
Теперь умножьте 4 на высоту, 4, и площадь составит 16 дюймов в квадрате.
Площадь неправильных фигур
Некоторые четырехугольники не подходят под определение квадрата, прямоугольника, ромба, параллелограмма или трапеции. Стороны имеют неровную или неправильную длину. Один из способов найти область этих фигур — нарисовать линии внутри фигуры, чтобы создать фигуры, для которых область может быть легко решена.
Например, многие четырехугольники состоят из прямоугольников и треугольников.
Определите площадь треугольника ½ x b x h и определите площадь прямоугольника w x h. Сложите две области вместе, чтобы вычислить площадь всей формы.
Правильные и неправильные четырехугольники — определение, примеры
По сторонам все четырехугольники можно разделить на две группы: правильные и неправильные.
Правильный и неправильный четырехугольник
Что такое правильный четырехугольник
Правильный четырехугольник — это четырехугольник с четырьмя сторонами одинаковой длины и четырьмя углами одинаковой меры.
Пример : Квадрат — единственный правильный четырехугольник
Правильный четырехугольник
Что такое неправильный четырехугольник
Неправильный четырехугольник — это тип четырехугольника, у которого одна или несколько сторон неравной длины и один или несколько углов неравной меры.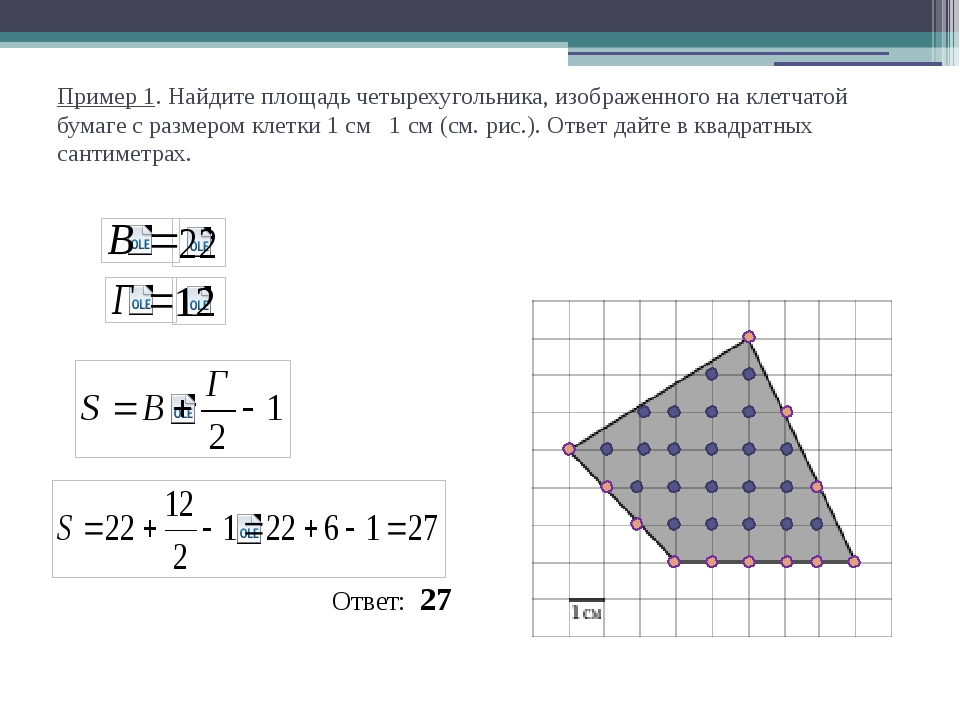
Примеры : прямоугольник, параллелограмм, ромб, трапеция и воздушный змей — неправильные четырехугольники.
Неправильный четырехугольник
Формулы
Площадь правильного четырехугольника
Квадрат — единственный известный нам правильный четырехугольник.Таким образом, чтобы найти площадь правильного четырехугольника, воспользуемся формулой определения площади квадрата. Формула приведена ниже:
Формула
Площадь (A) = a 2 , здесь a = сторона
В правильном четырехугольнике ABCD,
a = AB = BC = CD = DA
Найдите площадь правильного четырехугольника ABCD, стороны которого равны 12 м.
Решение:
Как известно,
Площадь ( A ) = a 2 , здесь a = 12 м
= 12 x 12 м 2
= 144 м 2
Площадь неправильного четырехугольника
Поскольку все неправильные четырехугольники имеют разную форму, мы не можем применить формулу какого-либо конкретного четырехугольника, чтобы найти площадь всех неправильных четырехугольников.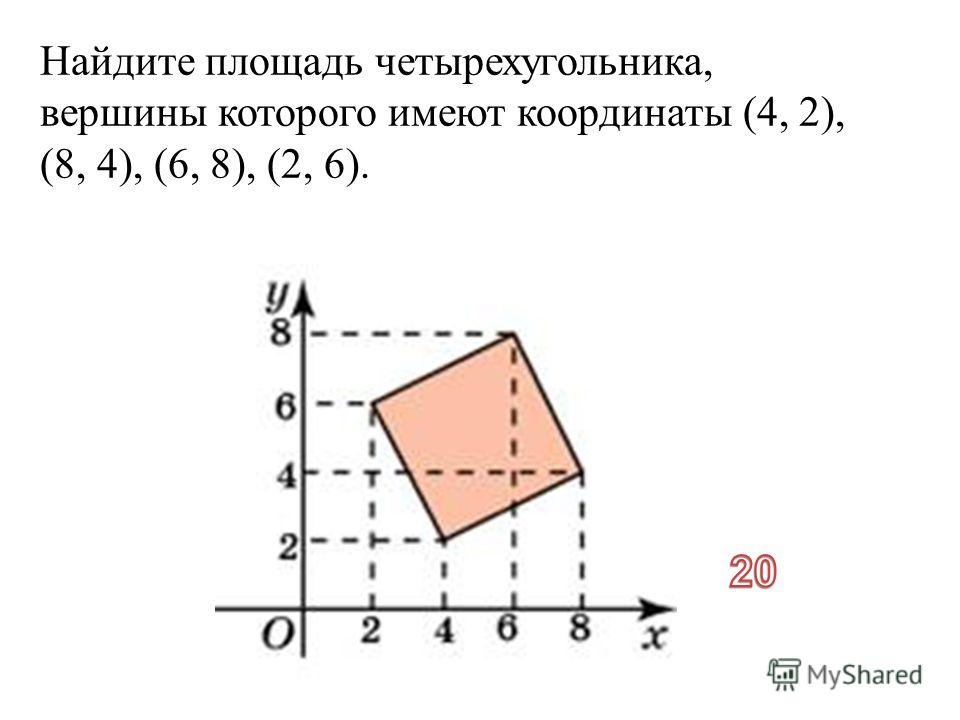 Другими словами, у нас нет фиксированной общей формулы, которую можно было бы использовать для всех из них. В таких случаях выполняются следующие шаги:
Другими словами, у нас нет фиксированной общей формулы, которую можно было бы использовать для всех из них. В таких случаях выполняются следующие шаги:
- Четырехугольник разделен на два треугольника путем рисования диагонали
- Найдите площадь каждого треугольника, используя разные формулы, как описано в нашей статье о треугольниках
- Добавьте площади двух треугольников
Шаги, хотя звучит легко, иногда могут быть довольно разрабатывать. Давайте возьмем пример, чтобы лучше понять концепции.
Найдите площадь неправильного четырехугольника ABCD со сторонами BC = 6 см, CD = 8 см, DA = 10 см и AB = 12 см и ∠BCD = 120 °.
Решение:
Разобьем неправильный четырехугольник ABCD на △ BCD и △ DAB, нарисовав диагональ BD
. Поскольку мы не знаем высоты ни одного из треугольников BCD и DAB, мы не можем использовать общую формулу . ½ x основание x высота , для определения площади треугольников.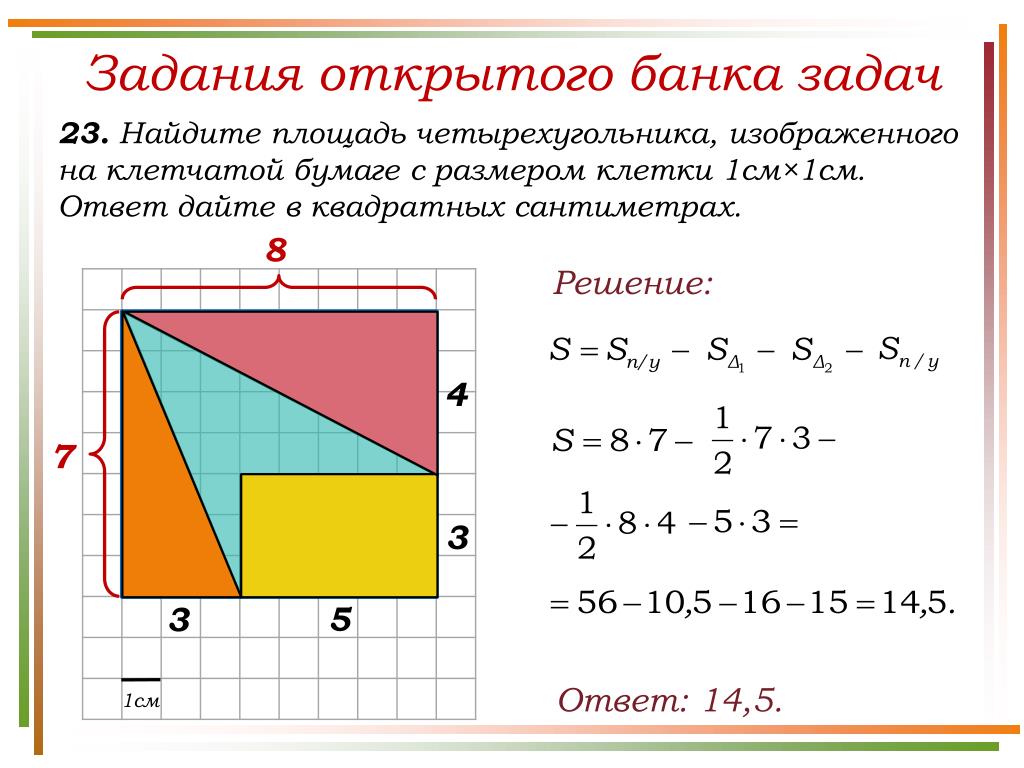
Использование закона бокового угла-стороны (SAS)
Здесь мы будем использовать тригонометрическую функцию ( A ) = ½ x BC x CD x sin C , чтобы вычислить площадь △ BCD
A = ½ x 6 x 8 x sin 120 °
= ½ x 48 x √3 / 2 см 2
= 20.78 см 2
Использование закона косинусов
Теперь мы знаем площадь △ BCD, но все еще не знаем длину диагонали BD. Для этого мы будем использовать закон косинусов :
c 2 = a 2 + b 2 — 2ab cos C
In △ BCD, пусть BC = h, CD = a и BD = t
Тогда приведенный выше закон косинусов можно записать как,
t 2 = a 2 + h 2 — 2ah cos T
t 2 = (8 x 8) + (6 x 6) — 2 x 8 x 6 cos 120 ° см
t 2 = 64 + 36 — (96 x cos 120 °) см
t 2 = 100 — (96 x (-0.5)) см
t 2 = (100 + 48) см
t 2 = 148 см
t = 12,165 см
Теперь у нас есть приблизительная длина диагонали BD, равная 12,165 см неправильного четырехугольника ABCD.
Использование формулы Герона
Зная диагональ четырехугольника ABCD, теперь мы можем вычислить площадь другой части четырехугольника, используя формулу Герона.
Поскольку формула Герона зависит от знания полупериметра, для △ DAB три стороны следующие:
DA = 10 см, AB = 12 см и BD = 12.165 см
Как известно, полупериметр ( с ) = ½ (10 + 12 + 12,165)
= 34,165 / 2 см
= 17,08 см
Теперь, применяя формулу Герона для расчета площади △ DAB,
A = √s (s — a) (s — b) (s — c) , здесь s = 17,08 см, a = 10 см, b = 12,165 см и c = 12 см
= √17,08 x ( 17,08 — 10) x (17,08 — 12,165) x (17,08 — 12) см 2
= √17,08 x 7,08 x 4,915 x 5,08 см 2
= √3019,314 см 2
= 54,948 см 2
Теперь, чтобы получить площадь неправильного четырехугольника ABCD, нам нужно сложить площадь треугольников BCD и DAB
Следовательно, площадь неправильного четырехугольника ABCD = Площадь △ BCD + Площадь △ DAB
= (20.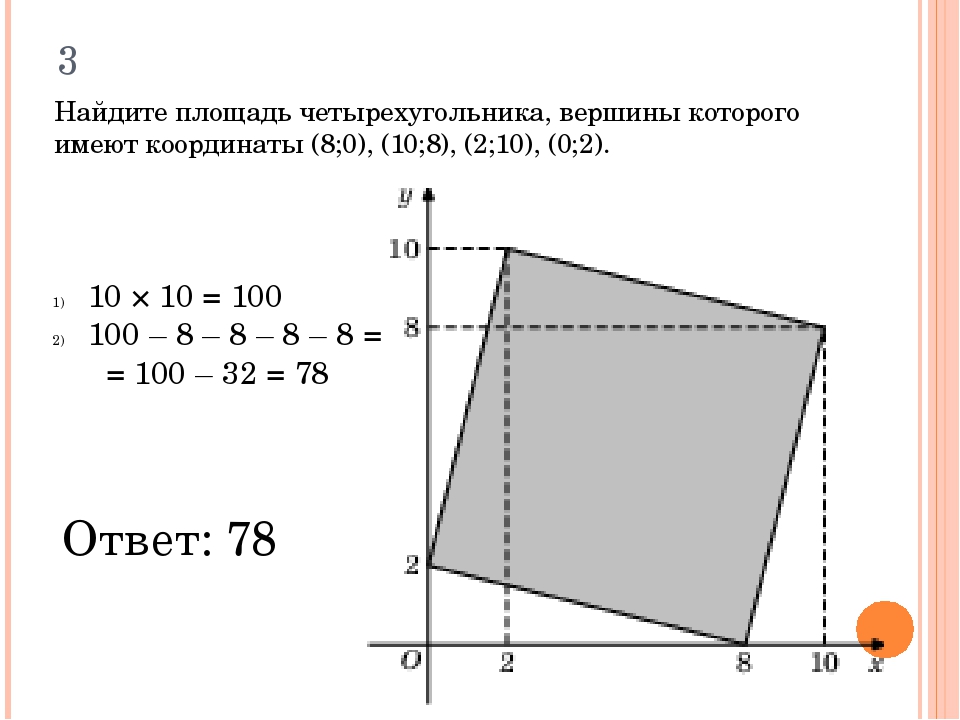 78 + 54,948) см 2
78 + 54,948) см 2
= 75,728 см 2
Часто задаваемые вопросы
1 кв. Назовите четырехугольник с четырьмя равными сторонами, который не является правильным?
Ответ . Нет такого четырехугольника с четырьмя конгруэнтными сторонами, но неправильным, потому что единственный четырехугольник, у которого есть четыре конгруэнтные стороны, — это квадрат, который является правильным четырехугольником.
2 кв. Назовите равносторонний четырехугольник, который не является правильным?
Ответ .Ромб
Q3. Является ли трапеция правильным четырехугольником?
Ответ . Все четыре стороны трапеции не равны, поэтому это не правильный четырехугольник.
4 кв. Как еще называют правильный четырехугольник?
Ответ . Мы обычно называем правильный четырехугольник квадратом.
Q5. Какой четырехугольник является правильным многоугольником?
Ответ . Площадь
Q6.Сколько линий симметрии в правильном четырехугольнике?
Ответ . Квадрат, являющийся единственным правильным четырехугольником, имеет четыре линии симметрии.
Q7. Сколько сторон у правильного четырехугольника?
Ответ . У правильного четырехугольника четыре стороны.
Q8. Является ли прямоугольник правильным четырехугольником?
Ответ . Поскольку у прямоугольника равны только противоположные стороны, они не являются правильным четырехугольником.
9 кв. Ромб — это правильный четырехугольник?
Ответ . Поскольку у ромба не все четыре угла равны, они не являются правильным четырехугольником.
Q10.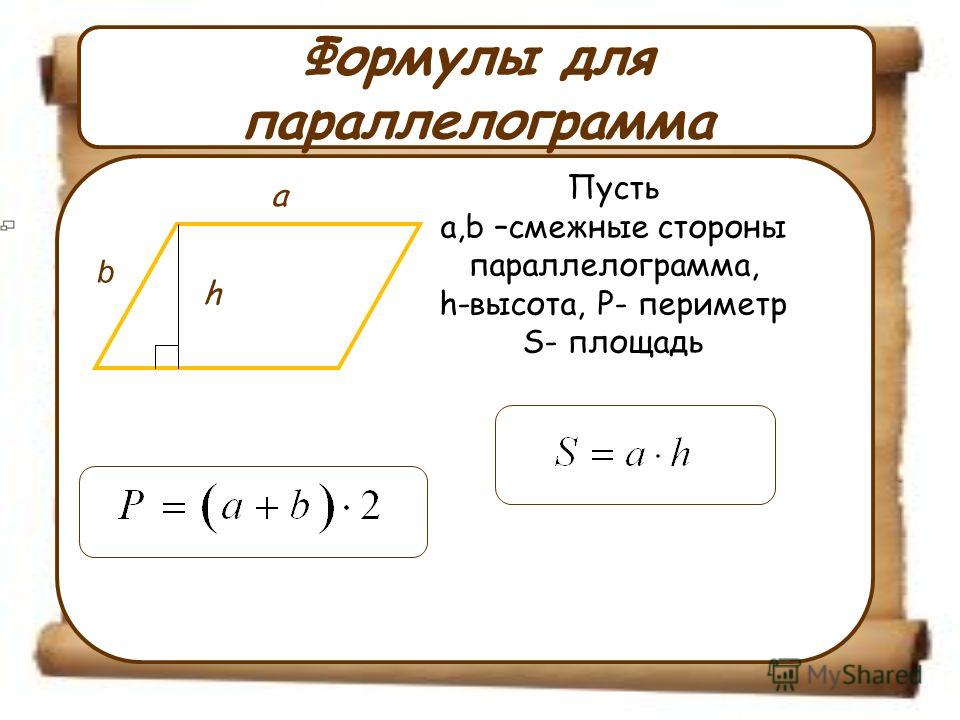 Назовите равносторонний четырехугольник, который не является правильным?
Назовите равносторонний четырехугольник, который не является правильным?
Ответ . Прямоугольник.
Q11. Может ли вогнутый четырехугольник быть правильным?
Ответ . Поскольку один из внутренних углов вогнутого четырехугольника превышает 90 °, невозможно получить вогнутый, но правильный четырехугольник.
Q12. У всех неправильных четырехугольников нет прямых углов?
Ответ . Единственный неправильный четырехугольник, имеющий прямые углы, — это прямоугольник.
Площадь четырехугольника — определение, формула и примеры
Площадь четырехугольника — это площадь внутри него. Напомним, что такое четырехугольник. Четырехугольник — это замкнутая форма, ограниченная четырьмя отрезками прямых. Четырехугольник может быть правильным или неправильным.Правильный четырехугольник — это четырехугольник, у которого все стороны равны. Неправильный четырехугольник называется неправильным четырехугольником. Четырехугольники бывают 6 видов.
Неправильный четырехугольник называется неправильным четырехугольником. Четырехугольники бывают 6 видов.
- квадрат
- прямоугольник
- параллелограмм
- трапеция
- ромб
- воздушный змей
На этой странице мы увидим, как найти площадь четырехугольника, разделив его на два треугольника, и как найти площадь четырехугольника, используя его 4 стороны.Кроме того, мы изучим формулы для определения площади каждого из этих четырехугольников разных типов.
Что такое площадь четырехугольника?
Площадь четырехугольника — это не что иное, как область, ограниченная сторонами четырехугольника. Он измеряется в квадратных единицах, таких как м 2 , в 2 , см 2 и т. Д. Процесс определения площади четырехугольника зависит от его типа и имеющейся информации о четырехугольнике.Если четырехугольник не принадлежит ни к одному из упомянутых выше типов, то мы можем найти его площадь, либо разделив его на два треугольника, либо используя формулу (которая называется формулой Бретшнайдера) нахождения площади четырехугольника используя четыре стороны.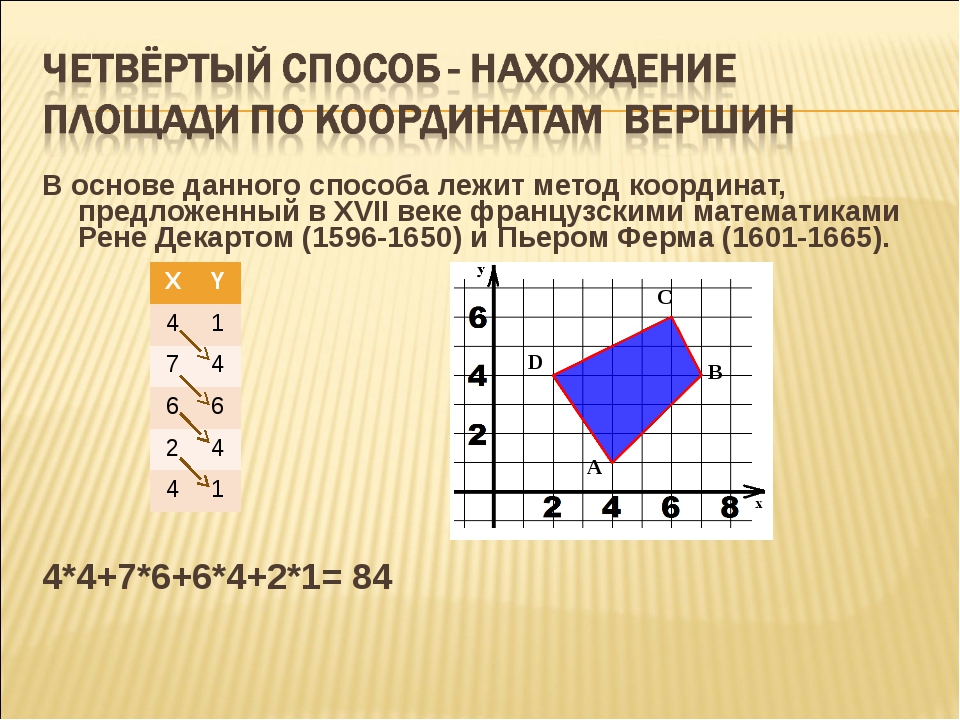 Здесь вы можете увидеть формулы для определения площади четырехугольника, не принадлежащего ни к одному из стандартных типов.
Здесь вы можете увидеть формулы для определения площади четырехугольника, не принадлежащего ни к одному из стандартных типов.
Давайте узнаем больше об этих формулах в следующих разделах.
Площадь четырехугольника, полученная при делении на два треугольника
Рассмотрим четырехугольник ABCD, в котором длина диагонали BD, как известно, равна «d».ABCD можно разделить на два треугольника диагональю BD. Чтобы найти его площадь, мы должны знать высоту треугольников ABD и BCD. Предположим, что высоты треугольников BCD и ABD равны \ (h_1 \) и \ (h_2 \) соответственно. Мы найдем площадь четырехугольника ABCD, сложив площади треугольников BCD и ABD.
Здесь площадь треугольника BCD = (1/2) × d × \ (h_1 \).
Площадь треугольника ABD = (1/2) × d × \ (h_2 \).
Из приведенного выше рисунка площадь четырехугольника ABCD = площадь ΔBCD + площадь ΔABD.
Таким образом, площадь четырехугольника ABCD = (1/2) × d × \ (h_1 \) + (1/2) × d × \ (h_2 \) = (1/2) × d × (\ (h_1 + h_2 \)).
Таким образом, формула, используемая для определения площади четырехугольника, когда заданы одна из его диагоналей и высоты треугольников (образованных данной диагональю), равна,
Площадь = (1/2) × Диагональ × (Сумма высот)
Площадь четырехугольной формулы с использованием сторон
Когда заданы стороны четырехугольника и два его противоположных угла, мы можем найти его площадь, используя формулу Бретшнейдера.{2} \ frac {\ theta} {2}} \), где
- s = полупериметр четырехугольника = (a + b + c + d) / 2
- θ = θ \ (_ 1 \) + θ \ (_ 2 \)
Площадь четырехугольника по формуле Герона
По формуле Герона, площадь треугольника с 3 сторонами a, b и c равна \ (\ sqrt {s (sa) (sb) (sc)} \), где ‘s’ — полупериметр треугольник, т. е. s = (a + b + c) / 2. Чтобы найти площадь четырехугольника по формуле Герона,
- Разделите его на два треугольника по диагонали (используйте диагональ, длина которой известна).

- Примените формулу Герона для каждого треугольника, чтобы найти его площадь.
- Добавьте площади двух треугольников, что даст площадь четырехугольника.
Формулы площади четырехугольников различных типов
Мы уже узнали, что существует 6 типов четырехугольников: квадрат, прямоугольник, параллелограмм, трапеция, ромб и воздушный змей. У нас есть специальная формула для определения площади каждого из этих четырехугольников.Посмотрим на них.
Часто задаваемые вопросы о четырехугольнике
Что такое площадь четырехугольника?
Площадь четырехугольника — это область, которая им окружена. Он измеряется в квадратных единицах, например: 2 , см 2 , м 2 и т. Д.
Что такое площадь четырехугольной формулы?
Площадь четырехугольника можно найти, разделив его на два треугольника по диагонали. Когда длина диагонали и высота двух треугольников известны, площадь (A) четырехугольника равна A = (1/2) × диагональ × (сумма высот). {2} \ frac {\ theta} {2}} \), где s — полупериметр четырехугольника. т.е. s = (a + b + c + d) / 2.
{2} \ frac {\ theta} {2}} \), где s — полупериметр четырехугольника. т.е. s = (a + b + c + d) / 2.
Как найти площадь четырехугольника по формуле Герона?
Мы знаем, что площадь четырехугольника можно найти, разделив его на два треугольника по диагонали. Кроме того, мы знаем, что площадь треугольника с 3 сторонами можно найти по формуле Герона. Используя формулу Герона, площадь треугольника со сторонами a, b и c определяется как \ (\ sqrt {s (sa) (sb) (sc)} \), где ‘s’ — это полупериметр треугольник.т.е. s = (a + b + c) / 2. Используя эту формулу, мы можем найти площади двух треугольников (которые образованы четырехугольником) и сложить их, чтобы получить площадь четырехугольника.
Какие формулы для определения площадей четырехугольников разных типов?
Существуют разные формулы для определения площадей четырехугольников разных типов. Их:
- Площадь квадрата со стороной «x» равна x 2 .
- Площадь прямоугольника размеров l и b равна l × b.
- Площадь параллелограмма с основанием «b» и высотой «h» равна b × h.
- Площадь трапеции, параллельные стороны которой равны ‘a’ и ‘b’, а высота (перпендикулярное расстояние между ‘a’ и ‘b’) ‘h’ равно (1/2) (a + b) h.
- Площадь ромба диагоналей d \ (_ 1 \) и d \ (_ 2 \) равна (1/2) × d \ (_ 1 \) × d \ (_ 2 \).
- Площадь воздушного змея с диагональю d \ (_ 1 \) и d \ (_ 2 \) равна (1/2) × d \ (_ 1 \) × d \ (_ 2 \).
Как найти площадь четырехугольника с координатами?
Когда вершинам четырехугольника заданы координаты, сначала найдите 4 длины сторон и длину диагонали, используя формулу расстояния.Затем разделите четырехугольник на две части, используя найденную вами диагональ, найдите площадь каждого треугольника, используя формулу Герона, а затем сложите площади двух треугольников, что даст площадь четырехугольника.
Площадь неправильной формы
Чтобы найти область неправильной формы, первое, что нужно сделать, это разделить неправильную форму на правильные формы, которые вы можете распознать, например
треугольники, прямоугольники, круги, квадраты и так далее …
Затем найдите площадь этих отдельных фигур и сложите их!
Пример № 1:
Фигура выше имеет две правильные формы.Он состоит из квадрата и полукруга
Найдите площадь для каждой из этих двух фигур и сложите результаты
Квадрат
Площадь квадрата = s 2
Площадь квадрата = 4 2
Площадь квадрата = 16
Круг
Площадь круга = pi × r 2
Обратите внимание, что радиус круга равен 4/2 = 2
Площадь круга = 3,14 × 2 2
Площадь круга = 3.14 × 4
Площадь круга = 12,56
Так как у вас есть только половина круга, вам нужно умножить результат на 1/2
Площадь полукруга = 1/2 × 12,56 = 6,28
Площадь эта форма = 16 + 6,28 = 22,28
Пример № 2:
Фигура выше имеет три правильные формы. Начиная сверху вниз, он имеет треугольник, прямоугольник,
и трапеция
Найдите площадь для каждой из этих трех фигур и сложите результаты
Треугольник
Площадь треугольника = (основание × высота) / 2
Площадь треугольника = (3 × 4) / 2
Площадь треугольника = 12/2
Площадь треугольника = 6
Прямоугольник
Площадь прямоугольника = длина × ширина
Площадь прямоугольника = 3 × 10
Площадь прямоугольника = 30
Трапеция
Площадь трапеции = ((b 1 + b 2 ) × h) / 2
Площадь трапеции = ((3 + 5) × 2) / 2
Площадь трапеции = (8) × 2/2
Площадь трапеции = 16/2
Площадь трапеции = 8
Площадь этой формы = 6 + 30 + 8 = 44
Пример № 3 :
Область неправильных форм может быть такой же сложной, как этот последний пример, поэтому внимательно изучите ее!
Фигура выше имеет 4 правильные формы.В нем есть треугольник, два прямоугольника,
и полукруга
Найдите площадь для каждой из этих 4 фигур и сложите результаты
Прямоугольник
Площадь прямоугольника = длина × ширина
Площадь прямоугольника = (12 × 16)
Площадь прямоугольника прямоугольник = 192
Поскольку у нас есть два одинаковых прямоугольника, площадь равна 192 + 192 = 384
Треугольник
Обратите внимание, что самая длинная сторона прямоугольника — это основание треугольника, а короткая сторона прямоугольника. — высота треугольника
Итак,
Площадь треугольника = (основание × высота) / 2
Площадь треугольника = (16 × 12) / 2
Площадь треугольника = (192) / 2
Площадь треугольника = 96
Круг
Чтобы получить площадь полукруга, нам нужно знать диаметр
Обратите внимание, что диаметр — это гипотенуза прямоугольного треугольника, поэтому используйте теорему Пифагора, чтобы найти длину диаметра
900 02 c 2 = a 2 + b 2
c 2 = 12 2 + 16 2
c 2 = 144 + 256
c 2 = 400
c = √400
c = 20
Следовательно, диаметр равен 20.Поскольку диаметр равен 20, радиус равен 10
Площадь круга = pi × r 2
Площадь круга = 3,14 × 10 2
Площадь круга = 3,14 × 100
Площадь круга круг = 314
Поскольку у вас только полукруга, вам нужно умножить результат на 1/2
1/2 × 314 = 157
Площадь этой формы = 384 + 96 + 157 = 637
Здесь мы идем! Я надеюсь, что эти хорошие примеры были очень полезны, помогая вам получить области неправильной формы.
Есть вопросы, как получить участки неправильной формы? Свяжитесь со мной.
конгруэнтных сегментов
конгруэнтных сегментов
EMAT
6700
пользователем
Брэд Симмонс
Периметр и площадь неправильных форм
С помощью блокнота геометра найдите периметр и площадь
Неправильные формы.
Задача: Найдите периметр и площадь
рисунок ниже.
Это
было бы чрезвычайно полезно знать, что периметр прямоугольника вдвое больше
длина плюс вдвое больше ширины.
P
= 2L + 2W
Кроме того,
площадь прямоугольника равна длине, умноженной на ширину.
А
= LW
Решение
используя блокнот геометра:
Разделить
фигуру неправильной формы выше в прямоугольники.Это можно сделать в
много разных способов. Рисунок ниже делит неправильную форму на две части.
прямоугольники.
два прямоугольника — это прямоугольник ABFD и прямоугольник FCEG.
Как
многими другими способами можно разделить эту неправильную форму на прямоугольники?
Банка
его можно разделить более чем на два прямоугольника?
Для
набросок этой фигуры в альбоме Geometer, которым можно манипулировать, нажмите
здесь.
Кому
Найдите площадь неправильной фигуры, сначала найдите области прямоугольника ABFD
и прямоугольник FCEG.
1.
Выберите четыре угловых точки прямоугольника.
2.
Постройте четырехугольник в интерьере.
3.
Выберите четырехугольник и измерьте площадь.
Площадь неправильной формы — это площадь двух сложенных вместе прямоугольников.
Использование
функция вычисления меры в Sketchpad Geometer для добавления областей.
Периметр неправильной формы равен сумме
шесть сегментов вокруг фигуры.
1. Выберите конечные точки сегмента, который нужно измерить.
2. Измерьте расстояние.
3. Используйте
функция вычисления меры в Sketchpad Geometer для добавления расстояний.
Найдите периметр и площадь каждой неправильной формы
1. Нажмите
здесь для эскиза, которым можно манипулировать.
2.
Нажмите
здесь для эскиза, которым можно манипулировать.
3 .
Нажмите
здесь для эскиза, которым можно манипулировать.
Возврат
Определение области неправильных фигур
Результаты обучения
- Объедините области правильных форм, чтобы найти области неправильных форм.
Итак, мы нашли область для прямоугольников, треугольников, трапеций и кругов. Неправильная фигура — это фигура, не имеющая стандартной геометрической формы. Его площадь не может быть рассчитана ни по одной из стандартных формул площади. Но некоторые неправильные фигуры состоят из двух или более стандартных геометрических фигур. Чтобы найти площадь одной из этих неправильных фигур, мы можем разбить ее на фигуры, формулы которых нам известны, а затем сложить площади фигур.
, пример
Найдите площадь заштрихованной области.
Решение
Данный рисунок неправильный, но мы можем разбить его на два прямоугольника. Площадь заштрихованной области будет суммой площадей обоих прямоугольников.
Синий прямоугольник имеет ширину [латекс] 12 [/ латекс] и длину [латекс] 4 [/ латекс]. Красный прямоугольник имеет ширину [латекс] 2 [/ латекс], но его длина не указана. Правая часть рисунка — это длина красного прямоугольника плюс длина синего прямоугольника. Поскольку правая сторона синего прямоугольника имеет длину [латекс] 4 [/ латекс] единиц, длина красного прямоугольника должна быть [латекс] 6 [/ латекс] единиц.
Площадь рисунка [латекс] 60 [/ латекс] квадратных единиц.
Есть ли другой способ разделить эту фигуру на два прямоугольника? Попробуйте и убедитесь, что у вас такая же площадь.
, пример
Найдите площадь заштрихованной области.
Показать решение
Решение
Мы можем разбить эту неправильную фигуру на треугольник и прямоугольник. Площадь фигуры будет суммой площадей треугольника и прямоугольника.
Прямоугольник имеет длину [латекс] 8 [/ латекс] единиц и ширину [латекс] 4 [/ латекс] единиц.
Нам нужно найти основание и высоту треугольника.
Поскольку обе стороны прямоугольника [латекс] 4 [/ латекс], вертикальная сторона треугольника — [латекс] 3 [/ латекс], то есть [латекс] 7 — 4 [/ латекс].
Длина прямоугольника составляет [латекс] 8 [/ латекс], поэтому основание треугольника будет [латекс] 3 [/ латекс], то есть [латекс] 8 — 4 [/ латекс].
Теперь мы можем добавить области, чтобы найти площадь неправильной фигуры.
Площадь рисунка [латекс] 36,5 [/ латекс] квадратных единиц.
, пример
Трасса средней школы имеет форму прямоугольника с полукругом (полукругом) на каждом конце. Прямоугольник имеет длину [латекс] 105 [/ латекс] метров и ширину [латекс] 68 [/ латекс] метров. Найдите область, ограниченную дорожкой. Округлите ответ до ближайшей сотой.
Показать решение
Решение
Разобьем фигуру на прямоугольник и два полукруга.Площадь фигуры будет суммой площадей прямоугольника и полукругов.
Прямоугольник имеет длину [латекс] 105 [/ латекс] м и ширину [латекс] 68 [/ латекс] м. Полукруги имеют диаметр [латекс] 68 [/ латекс] м, поэтому каждый имеет радиус [латекс] 34 [/ латекс] м.
неправильных многоугольников
Обзор
Если вы просмотрели страницу, озаглавленную «Правильные многоугольники», вы можете вспомнить, что многоугольник — это замкнутая двумерная фигура с несколькими (т.е. три и более) прямых сторон. Поскольку правильный многоугольник — это такой многоугольник, у которого все стороны имеют одинаковую длину, а все внутренние углы имеют одинаковую величину, отсюда следует, что неправильный многоугольник не соответствует этим критериям (т. Е. не является ни равносторонним , ни равносторонним ). Подобно правильным многоугольникам, неправильные многоугольники могут быть простыми (т. Е. Выпуклыми или вогнутыми фигурами, в которых стороны образуют границу вокруг единого замкнутого пространства, и ни один внутренний угол не превышает ста восьмидесяти градусов) или сложными (два или более стороны будут пересекать друг друга).Ниже мы приводим несколько примеров неправильных многоугольников.
Примеры неправильных многоугольников
Здесь следует отметить, что набор неправильных многоугольников, помимо того, что он бесконечно велик, включает в себя ряд форм, с которыми вы, возможно, уже знакомы. Форма (a), например, представляет собой прямоугольник (и, следовательно, по определению также параллелограмм и четырехугольник ).Это нерегулярно в силу того, что, хотя противоположные стороны равны по длине, соседние стороны — нет. Форма (b) представляет собой равнобедренный треугольник , и он неправильный, потому что только две стороны равны, и только два угла равны. Форма (c) представляет собой параллелограмм и четырехугольник . Это нерегулярно, потому что смежные стороны не равны, а прилегающие углы не равны. Форма (d) представляет собой трапецию и четырехугольник . Он имеет две равные стороны и две пары равных углов, но явно неправильной формы.
Остальные формы действительно не имеют конкретных имен. Форма (e) представляет собой сложный четырехугольник , в котором нет двух равных сторон и нет двух равных углов. Форма (f) технически представляет собой шестиугольник (поскольку у него шесть сторон). Однако он имеет и неправильную форму, потому что у него стороны разной длины и углы разной величины, и вогнутый, потому что один из его внутренних углов больше ста восьмидесяти градусов (> 180 °).Точно так же форма (g) технически представляет собой пятиугольник , поскольку он имеет пять сторон, но никакие две стороны не имеют одинаковой длины, и только два из пяти внутренних углов одинаковы. Как и форма (f), форма (h) также представляет собой вогнутый шестиугольник, но в этом случае ни одна из сторон не равна, ни один из углов не равен, и никакие две стороны не параллельны.
Нахождение площади неправильного многоугольника
Как и в случае любого многоугольника, определение периметра является относительно тривиальным занятием.Если вам известна длина каждой стороны, вы можете просто сложить длины вместе, чтобы найти периметр. Если длина некоторых или всех сторон неизвестна, сначала необходимо определить длину каждой стороны, измерив ее. Найти область сложнее. В случае неправильных многоугольников, которые являются треугольниками или четырехугольниками, методы, которые можно использовать, описаны на соответствующих страницах. Для неправильных многоугольников, имеющих более четырех сторон, необходимо использовать другие методы. Точный метод, используемый в каждом конкретном случае, будет зависеть от типа неправильного многоугольника, с которым мы имеем дело.Рассмотрим, например, неправильный шестиугольник, показанный ниже.
Неправильный шестиугольник
В этом случае мы знаем, что отрезки AB и DE равны по длине, как и отрезки BC , CD , EF и FA . Мы также знаем, что отрезки AB, и DE параллельны.Из этой информации мы можем сделать вывод, что углы ABC и CDE равны, а углы DEF и FAB равны. Мы также можем сделать вывод, что углы ABC и FAB являются дополнительными (в сумме составляют сто восемьдесят градусов), как и углы CDE и DEF . Также можно показать, что отрезки BC и FA параллельны, как и отрезки CD и EF .Из этой информации вы должны увидеть, что если мы возьмем треугольную часть формы, определяемую точками B, C и D, и переместим ее так, чтобы она покрывала треугольную область, определенную точками A, E и F, мы останется прямоугольник, как показано ниже.
Неправильный шестиугольник превращается в прямоугольник.
Мы можем видеть, что неправильный шестиугольник ABCDEF эквивалентен по площади прямоугольнику ABCD, поэтому площадь ABCDEF можно найти, взяв произведение длин отрезков AB и BD .Если эти длины известны, это несложный расчет. В противном случае их необходимо сначала найти путем измерения. В случаях, подобных описанному выше, часто можно преобразовать неправильный многоугольник в форму, для которой у нас уже есть метод вычисления площади и которая имеет ту же площадь, что и исходная форма. В других случаях это либо сложно, либо невозможно. В качестве альтернативы мы могли бы нарисовать отрезок FC , как показано ниже, фактически разбив форму на два параллелограмма равной площади.Затем мы могли бы найти площадь одного из параллелограммов и умножить результат на два, чтобы найти общую площадь фигуры.
Неправильный шестиугольник можно разбить на два параллелограмма равной площади.
Один из методов, который работает для определения площади любого неправильного многоугольника (или любого правильного многоугольника , если на то пошло), включает разбиение многоугольника на треугольники, определение площади каждого треугольника стандартными методами и сложение площадей отдельных треугольников вместе. (обратите внимание, что в некоторых случаях фигуру можно разбить на комбинацию треугольников и прямоугольников, но все многоугольники можно разбить на треугольники).Принцип показан ниже.
Любой многоугольник можно разбить на несколько треугольных областей.
Площадь многоугольника складывается из площадей треугольников T1, T2, T3, T4, T5 и T6. Основным недостатком этого метода является то, что он будет включать выбор одной стороны каждого треугольника в качестве основания, построение перпендикулярного отрезка прямой от основания до вершины треугольника (т.е. угол напротив основания), и измерив размеры каждого. После того, как вы узнаете длину основания l и высоту h для каждого треугольника, можно легко вычислить площадь:
| Площадь = | л × h |
| 2 |
Существует также формула, с помощью которой можно найти площадь простого выпуклого или вогнутого неправильного многоугольника, даже если все стороны имеют разную длину и каждый угол разной величины.Однако формулу можно использовать только , если вам известны координаты каждой из вершин. У него также есть недостаток, заключающийся в том, что его нельзя использовать для сложных многоугольников (то есть многоугольников, в которых две или более стороны пересекаются друг с другом). Рассмотрим следующий вогнутый неправильный многоугольник:
Неправильный вогнутый шестигранный многоугольник
Координаты вершин неправильной шестигранной фигуры, показанной выше, следующие:
- А 2, 3
- В 4, 5
- С 7, 5
- Д 9, 1
- E 6, 2
- Ж 3, 1
Общая формула, используемая для определения площади простого многоугольника, использует координаты xy каждой вершины многоугольника от первой до последней в порядке по часовой стрелке вокруг формы следующим образом:
| Площадь = | ( x 1 y 2 — y 1 x 2 ) + ( x 09 2 9055 — y 2 x 3 ).. . + ( x n y 1 — y n x 1 ) |
| 2 |
9
Применяя формулу к нашему шестигранному неправильному многоугольнику, мы получаем:
| Площадь = | ( x A y B — y A x B ) + ( x B C — y B x C ) + ( x C y D — y C x D x y E — y D x E ) + ( x E y F — y E 9055 + F x x F y A — y F x A ) |
| 2 |
| Площадь = 3 985 4) + (4 · 5 — 5 · 7) + (7 · 1 — 5 · 9) + (9 · 2 — 1 · 6) + (6 · 1 — 2 · 3 ) + (3 · 3 — 1 · 2) |
| 2 |
| Площадь = | (10-12) + (20-35) + (7-45) + (18-6 ) + (6-6) + (9-2) |
| 2 |
| Площадь = | -2-15-38 + 12 + 0 + 7 |
| 2 |
Не волнуйтесь, если результат окажется отрицательным.Просто измените знак минуса на знак плюс. В качестве быстрой проверки результата вы можете вычислить площадь ограничивающего прямоугольника, поскольку полученный ответ всегда должен быть меньше этого числа. В этом случае площадь ограничивающего прямоугольника будет равна произведению 9-2 (то есть разницы между максимальной и минимальной координатами x ) и 5-1 (то есть разницы между максимальной и минимальной координатами y ). , что дает нам 7 × 4 = 28.
В качестве дополнительной проверки можно вычислить площади треугольников, образованных между периметром ограничивающего прямоугольника и периметром многоугольника, как здесь.Три треугольника, образованные таким образом в примере, который мы использовали, являются прямоугольными. Для этих треугольников мы знаем длины сторон, смежных с прямым углом, что, по сути, дает нам базовую длину и высоту. Мы также знаем длину основания и высоту оставшегося треугольника (треугольник DEF ), даже если этот треугольник не содержит прямого угла.

 Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины.
Аналогично, но уже с помощью определения синуса, можно определить длину второй стороны. А как найти площадь прямоугольника теперь? Да очень просто, перемножить полученные величины. Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так:
Полученный результат разделить на два и получим длину второй стороны. Ну, а дальше стандартный прием, перемножаем обе стороны и получаем площадь прямоугольника. В виде формулы это будет выглядеть так: